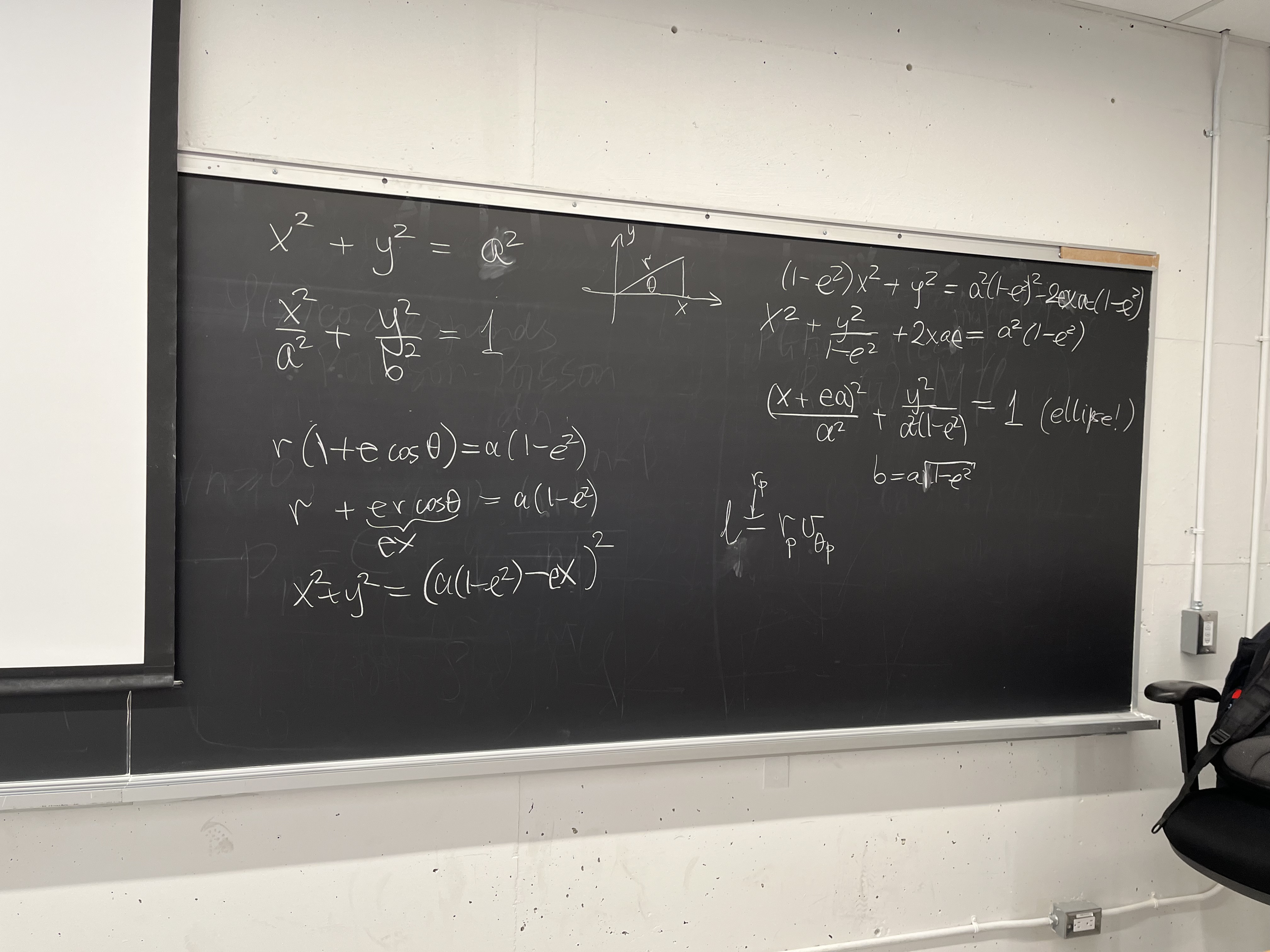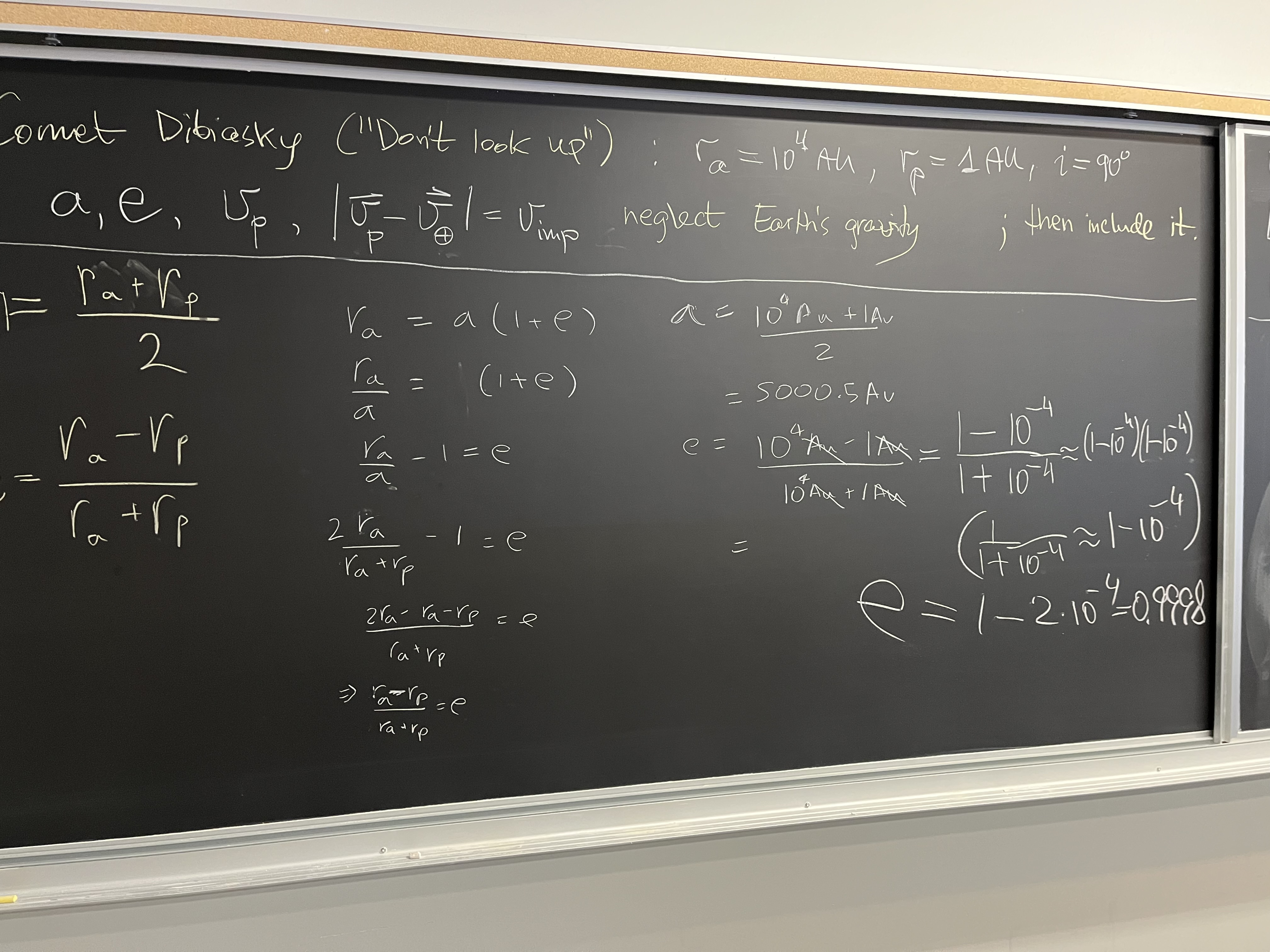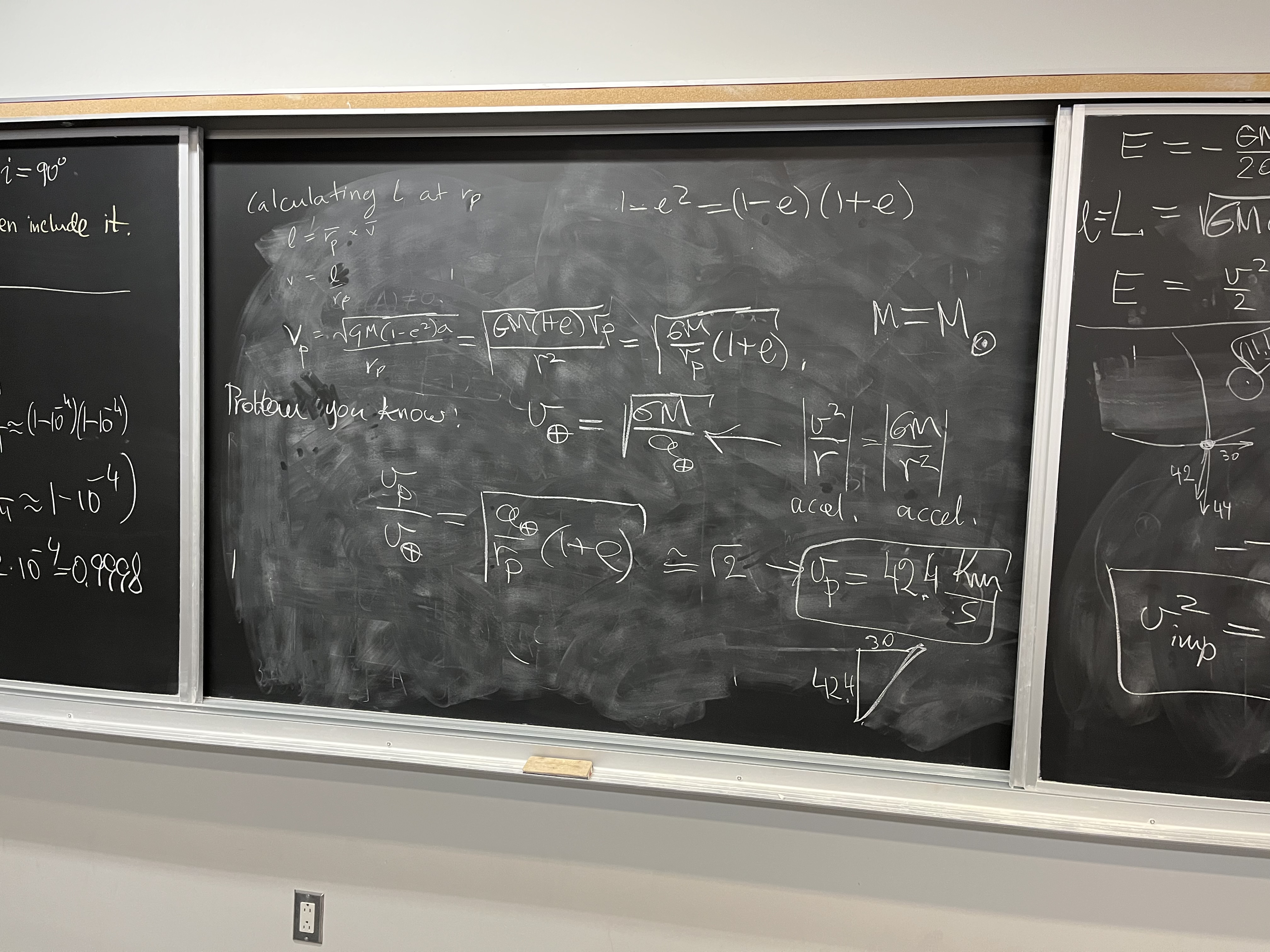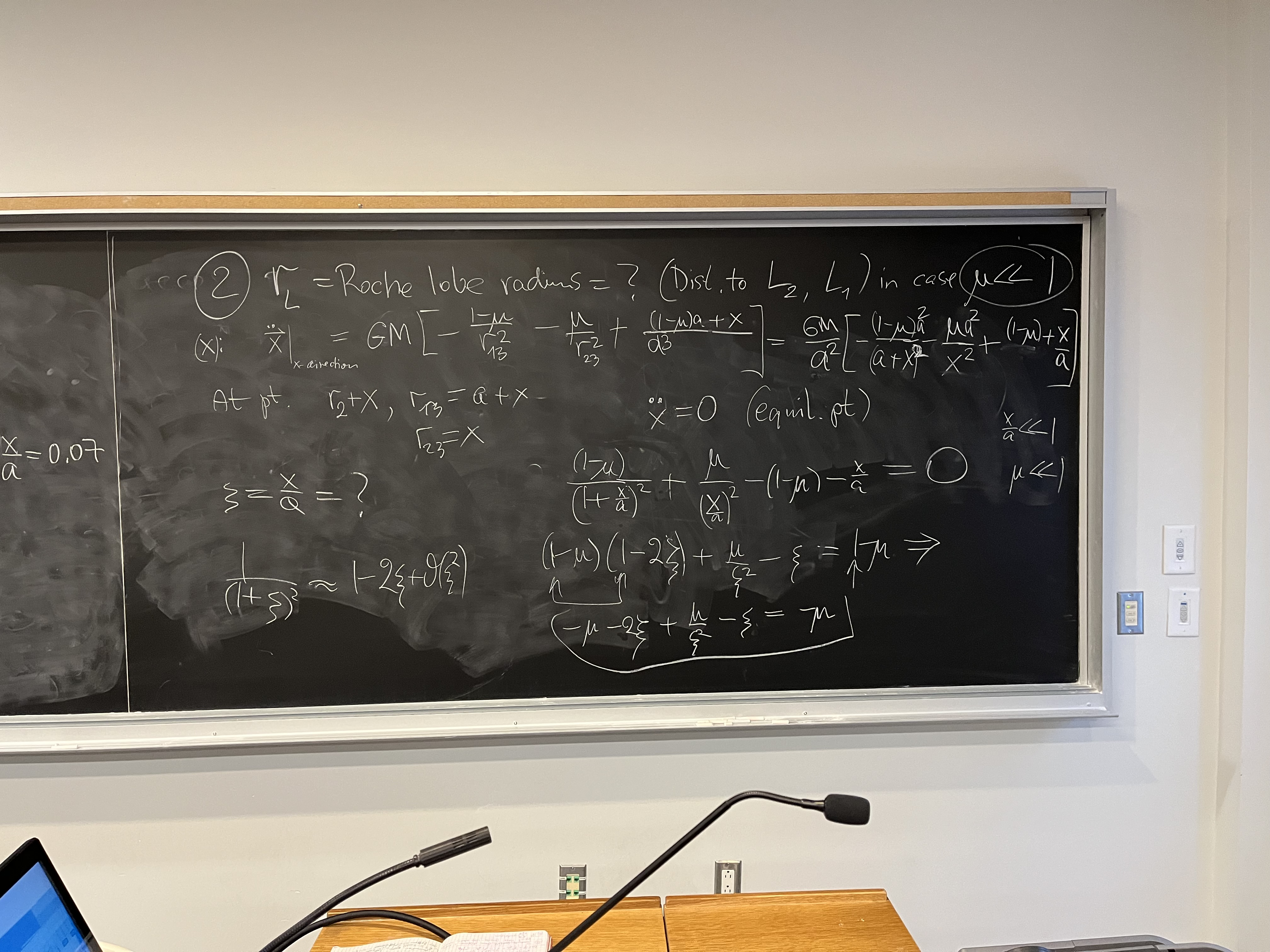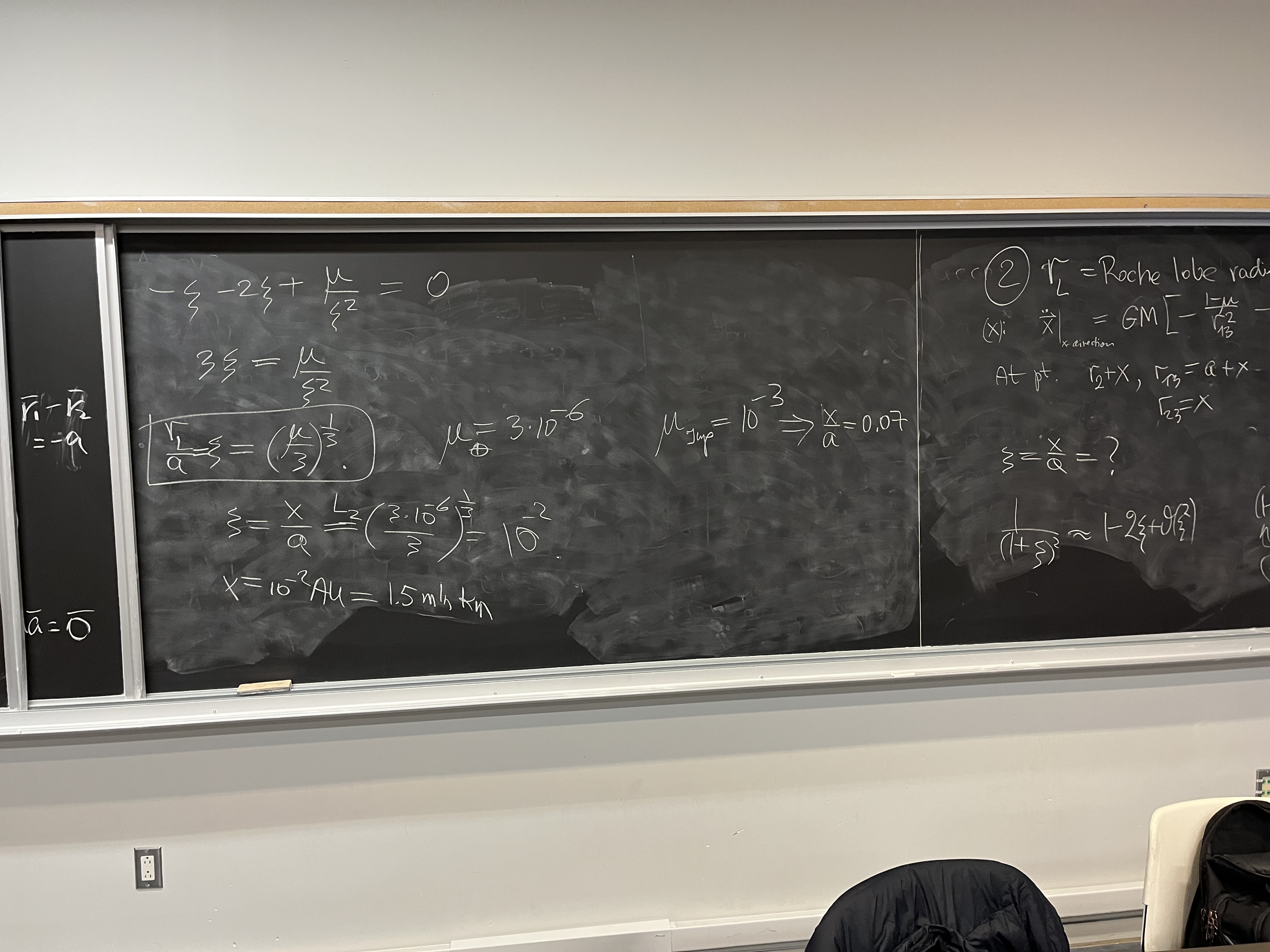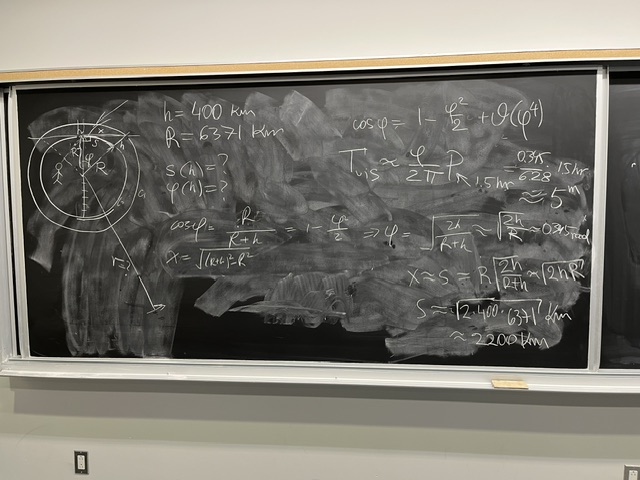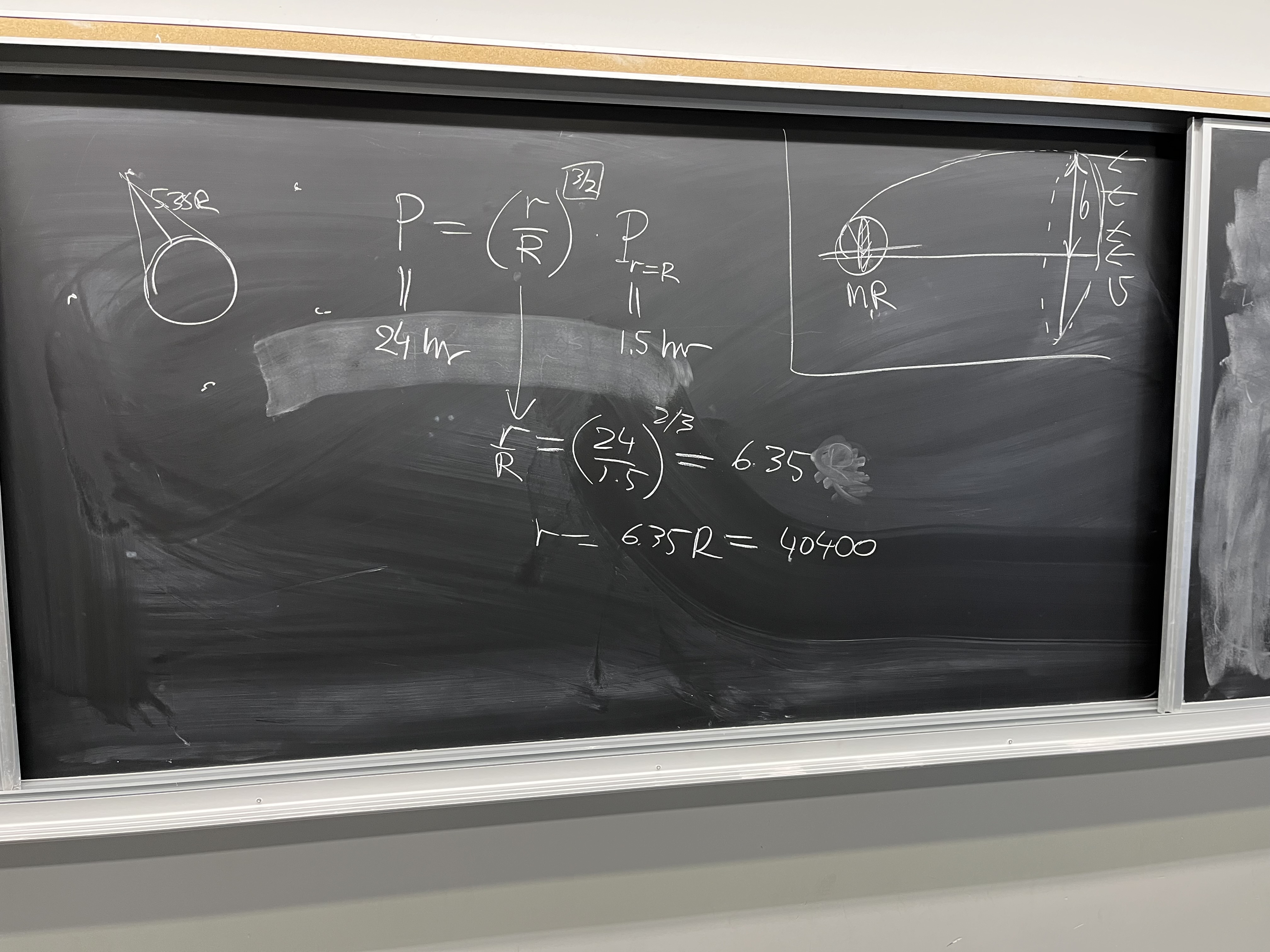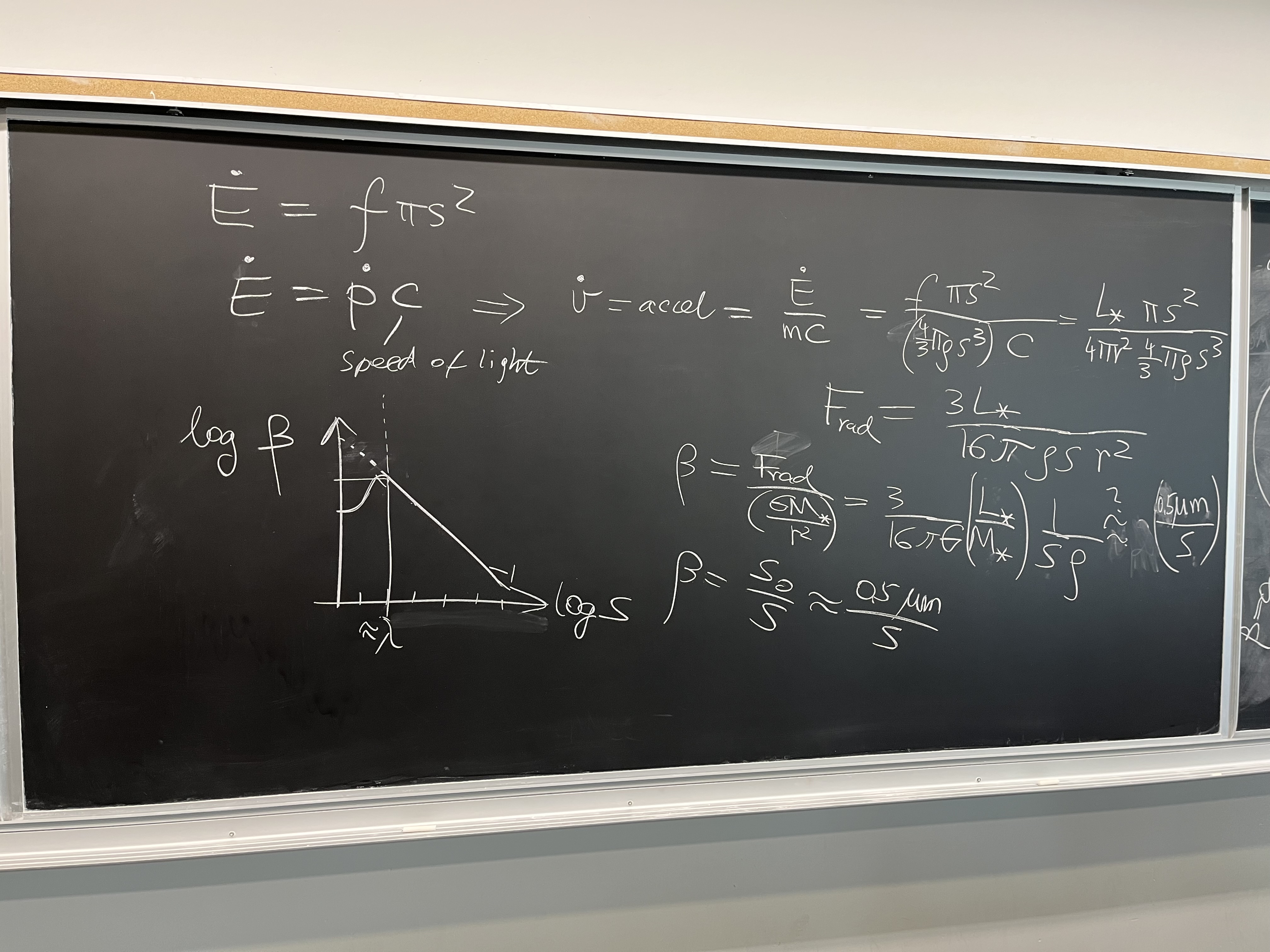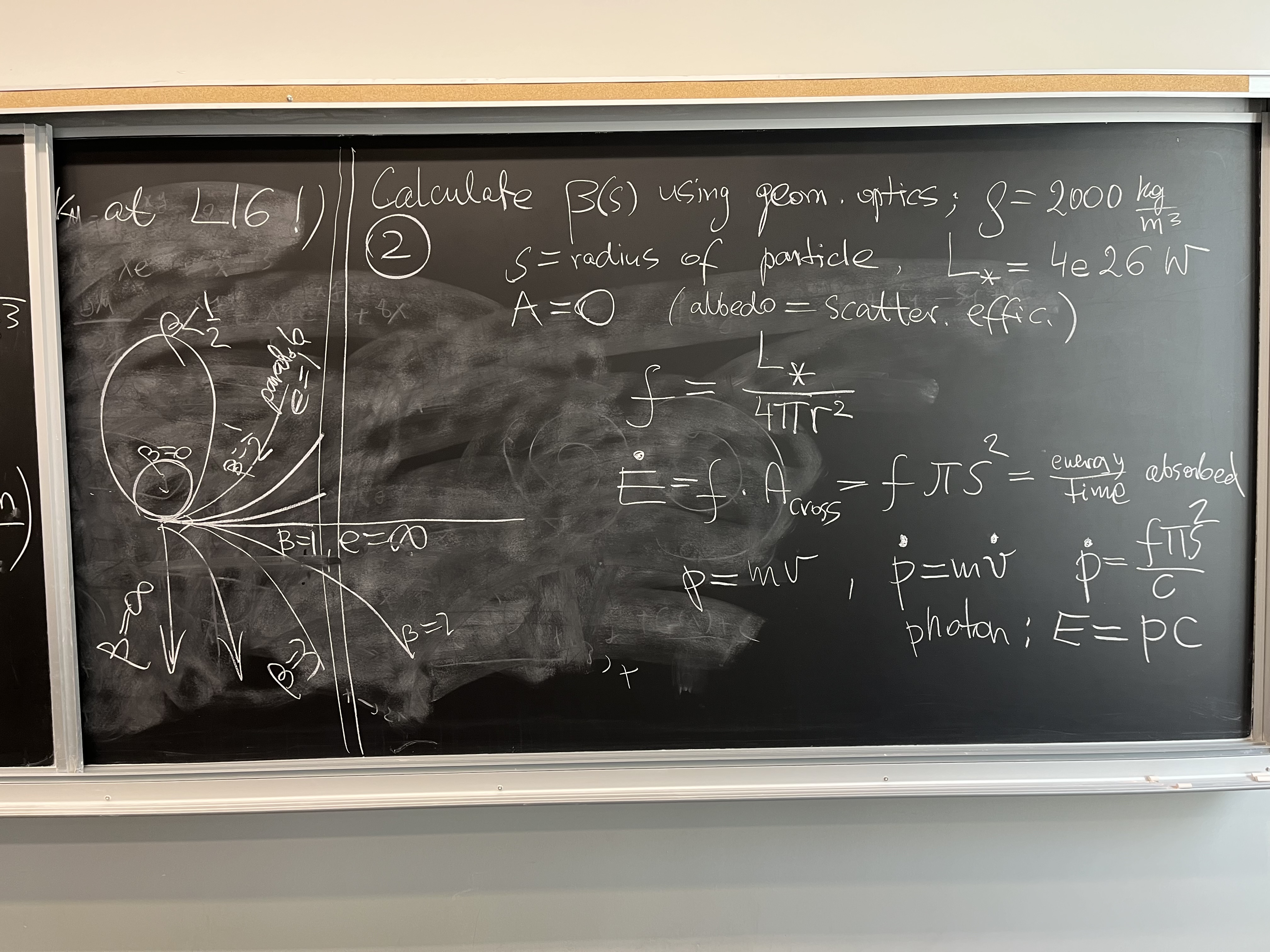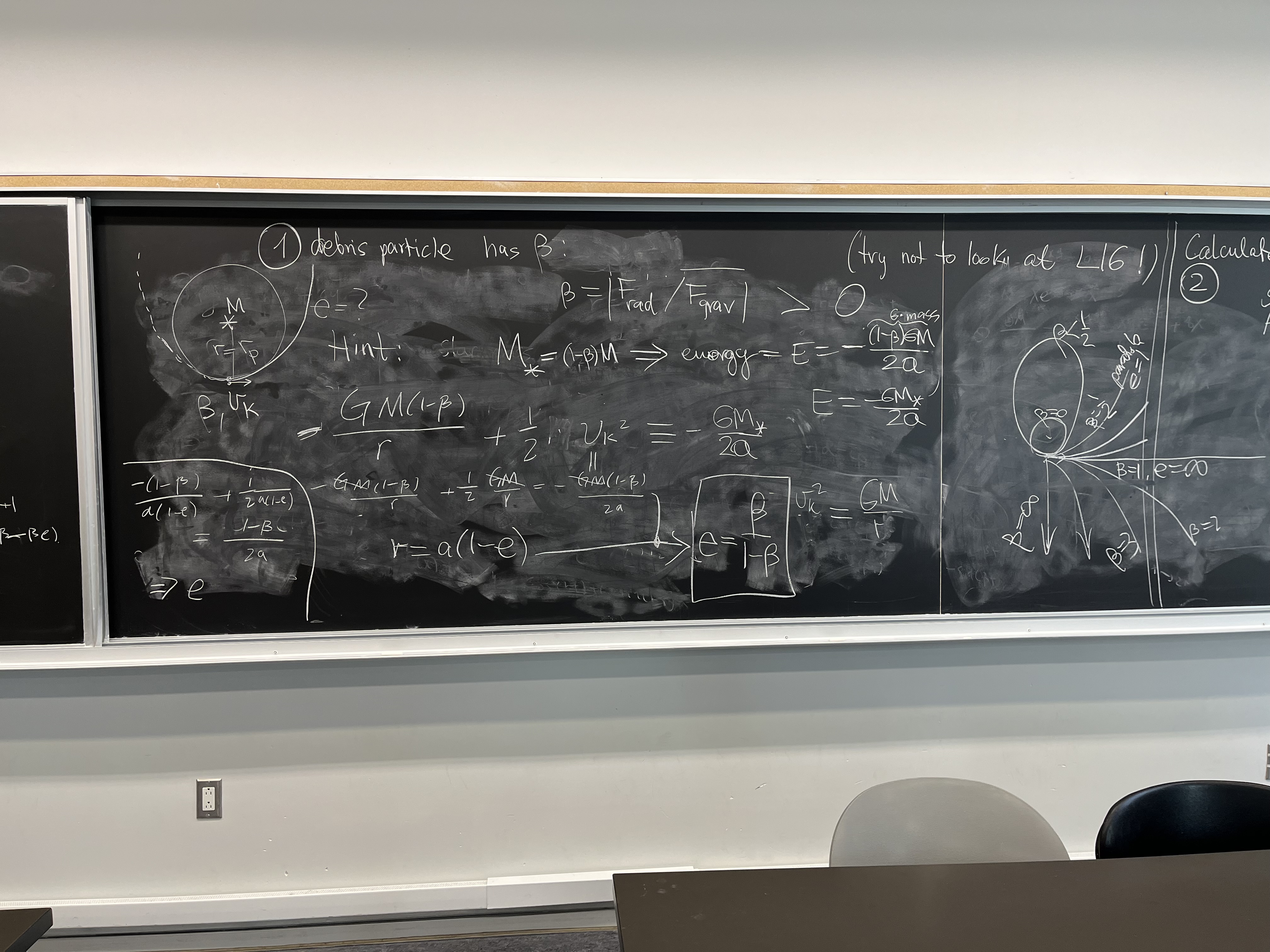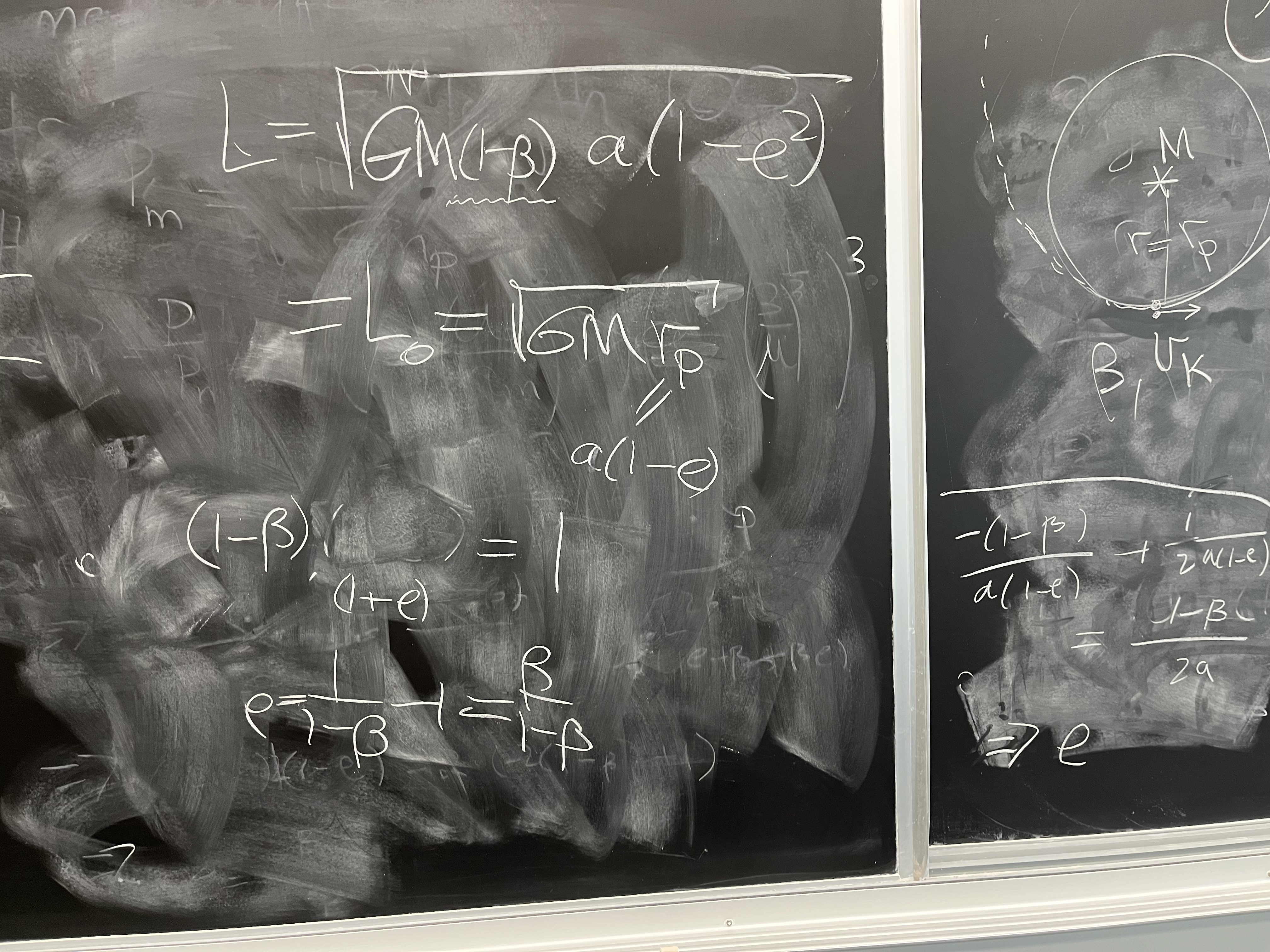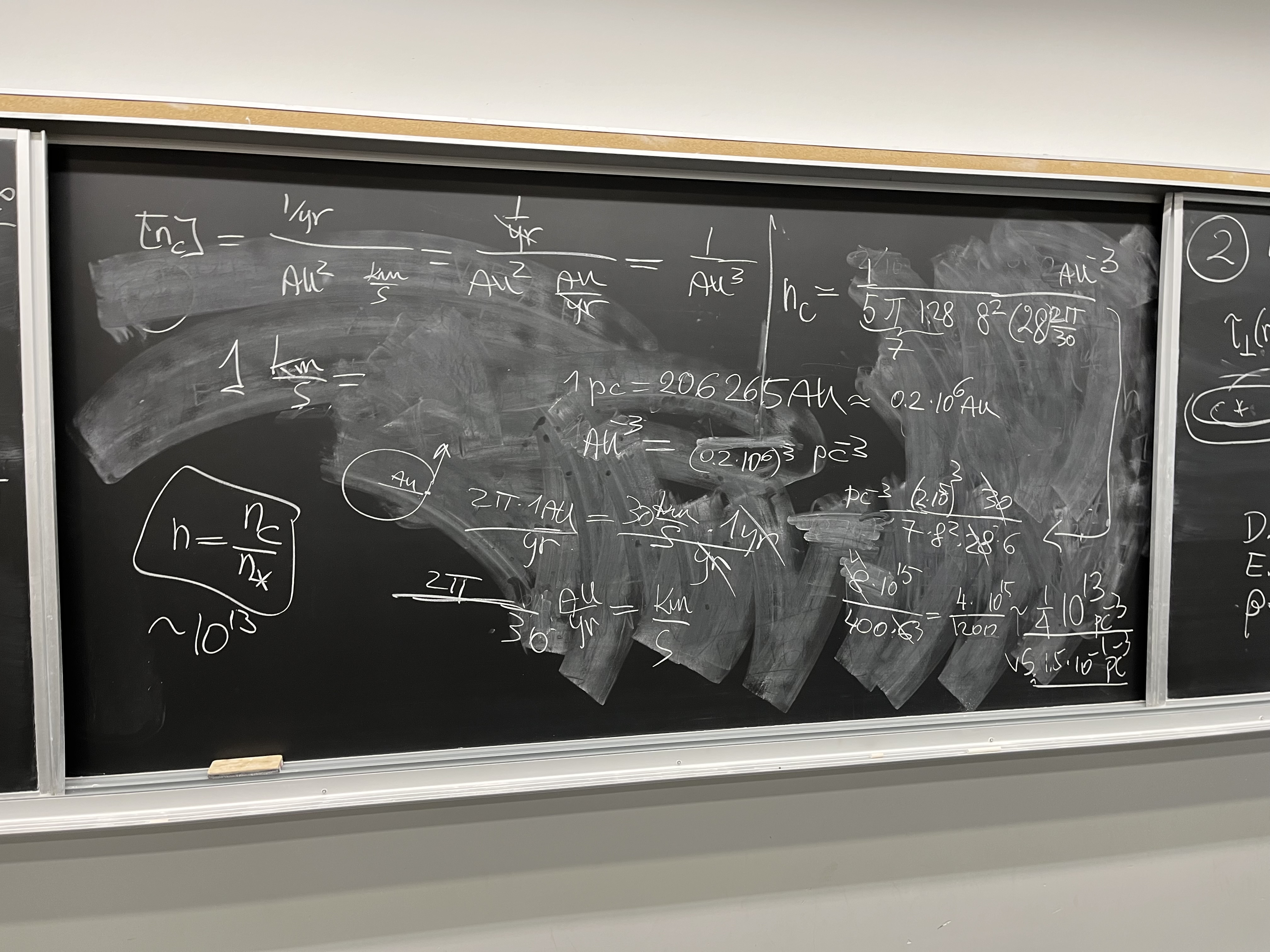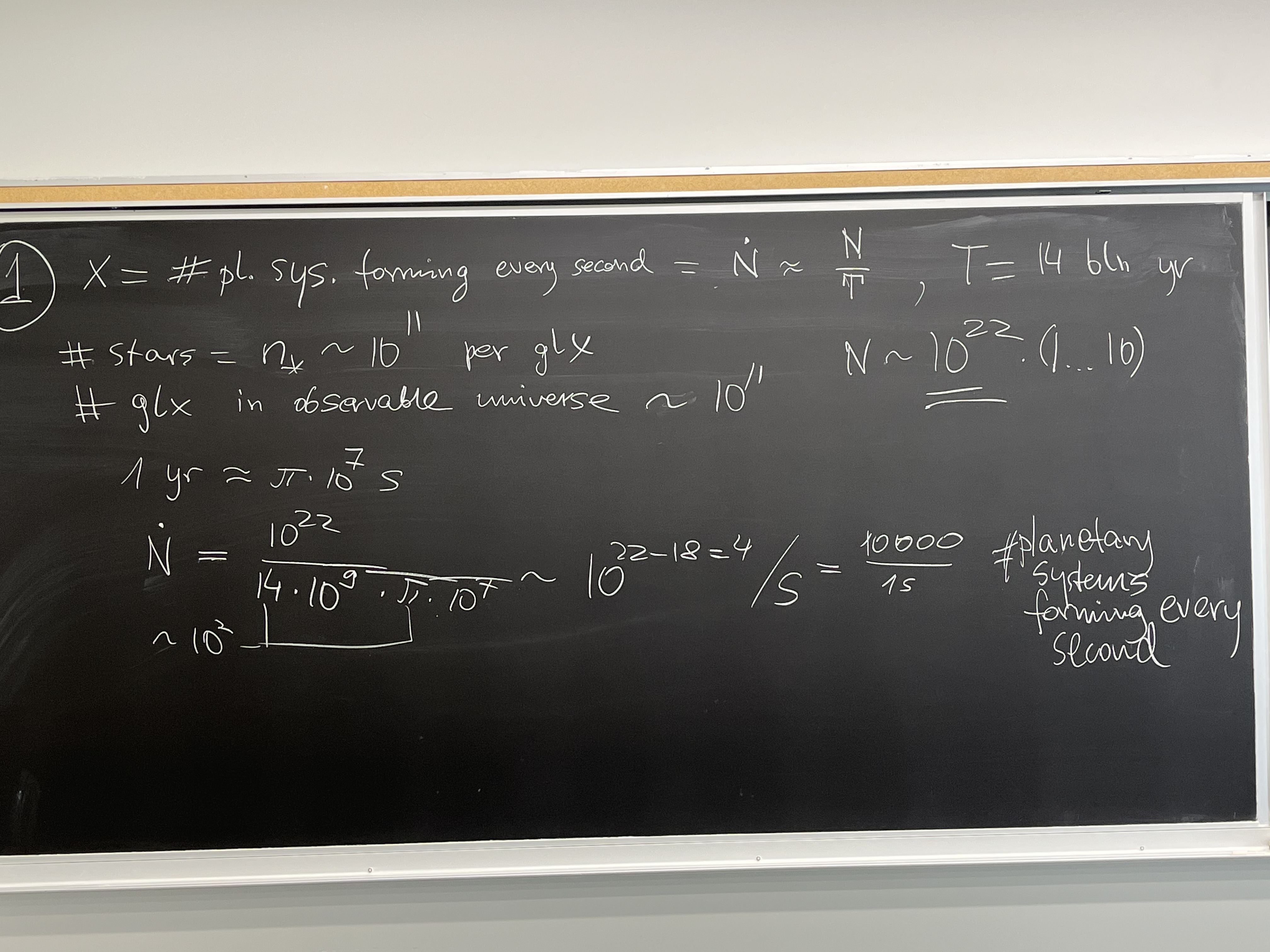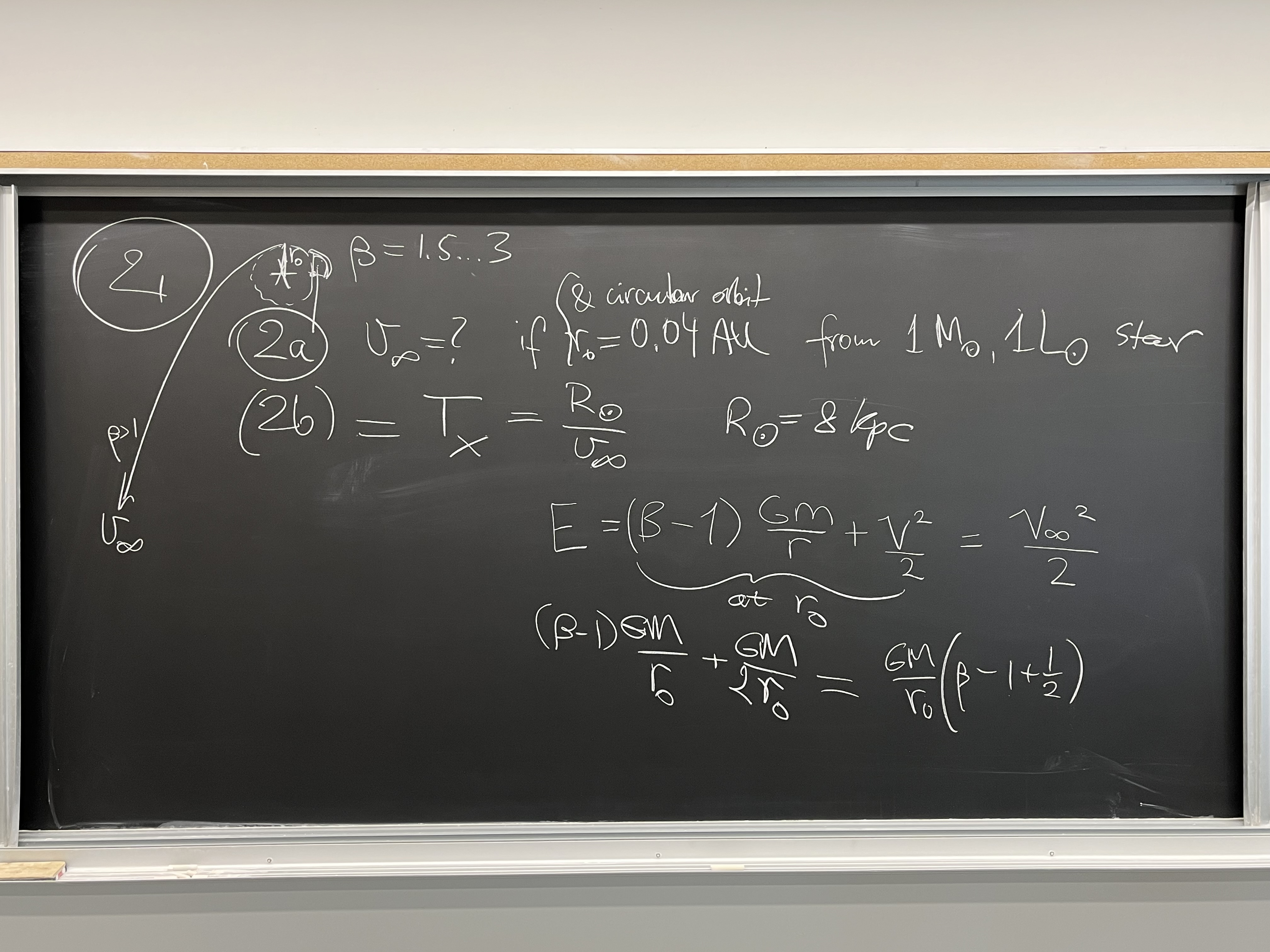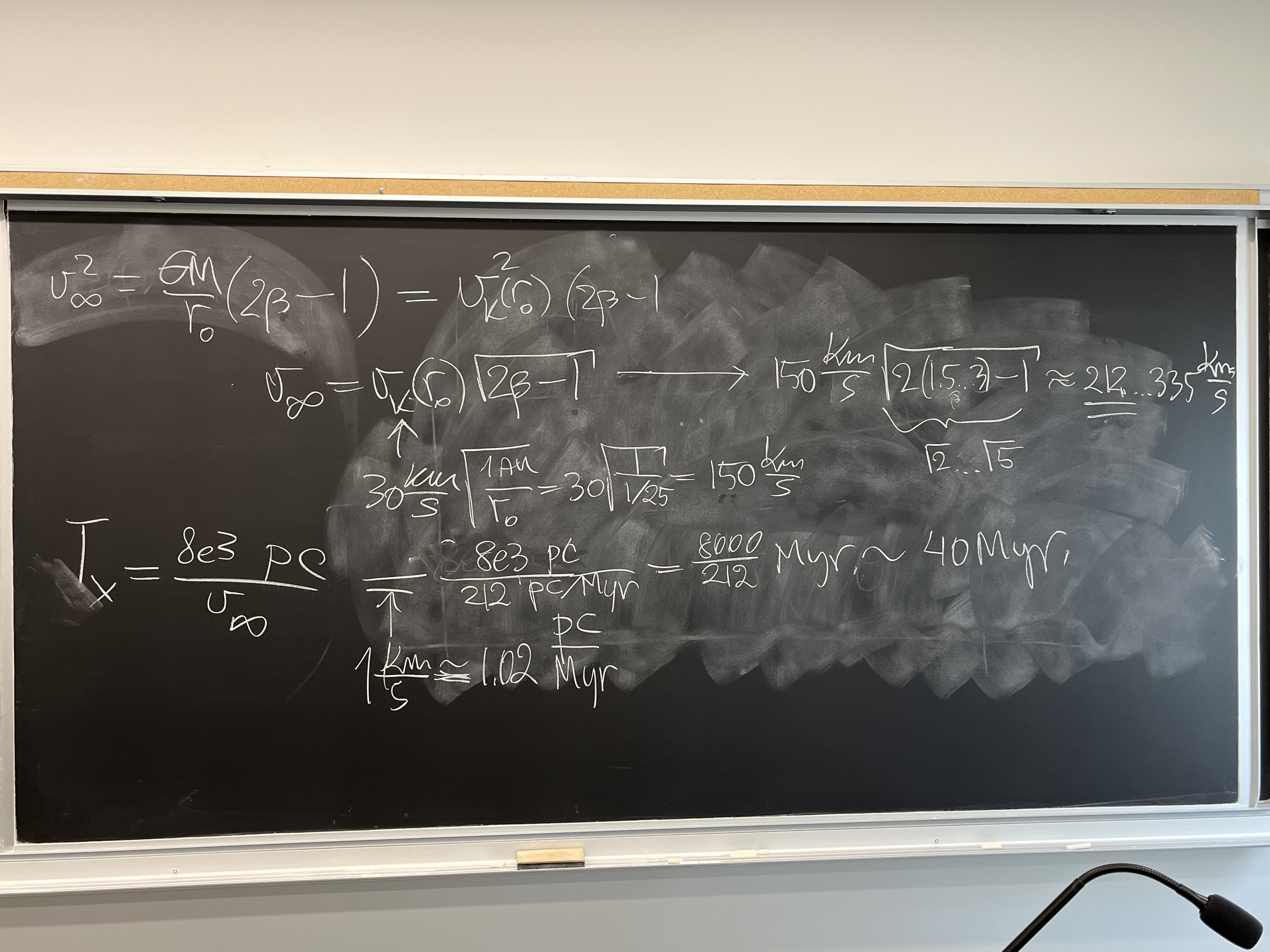Tutorials. ASTC25 2025
Tutorial 1 on 16 Jan 2025
Distance to Mars at a near-aphelic opposition today
Mars is very bright on the sky right now, like in every opposition, when
full planetary face is illuminated (like full Moon), and it is closest
to Earth in a given cycle. But there are different types of opposition,
depending on where they happen on Mars's fairly elliptical orbit around the
sun. By the way, you can see where the planets are in space right now here
in the orbit
viewer .
Assume the current opposition is aphelic (Sun, Earth and Mars line up
perfectly, in that order, and Mars is at aphelion). Calculate the distance
between Mars and Earth in AU and km, as well as in light-minutes.
Separately calculate the perihelic opposition distance when Mars is at
perihelion.
That is, give another formula, not just a number! If I want you to give a
numerical answer, I usually ask to "evaluate" something, while "find" or
"derive" means analytical answer, and "calculate" means both analytical formula
and numerical value. I am forgetful and may depart from this convension, but in
general I want you to show the derivations with some comments on what you are
doing, not just pure symbolic math, and definitely not just numbers.
Also calculate the maximum distance in 1/2 of synodic period (January next year)
when Mars will be in conjunction with the sun.
You are given the following data: $a_M = 1.524$ AU, 1 AU = 150 mln km,
$c = 0.3$ mln km/s (speed of light), $e_M = 0.0934$, $a_E = 1$ AU
(by definition), $e_E = 0.0167 \simeq 0$ (assume it's zero for this problem,
since Mars's eccentricity, $e_M\gg e_E$, is much larger and more important).
SOLUTION
We did a sketch of the situation with red chalk marking position of Mars,
talked about why Mars is a red planet, and then derived distance at opposition,
$d$, in two cases (a,p = aphelion, perihelion).
$$d_{a,p} = a_M(1\pm e_M) - a_E$$
Units (AU or other) check ok. Now we can substitute values:
$d_{a,p} = \{0.666, 0.382\}\; \mbox{AU} = \{100, 57.2\}\; \mbox{mln km}
= \{333, 191\}\; \mbox{light-seconds}.$
As you see, we kept 3 accurate digits in the answer only, since this many we
also had in the input data. Never quote a long string of numbers from a
calculator if that precision is not warranted by the precision of all inputs.
The last units (light-sec) are useful if you send a robotic rover to Mars and
are driving it. You'll need to wait at least that may second for a reaction,
and twice that to notice it after the signals are sent back to Earth.
Brightness difference of Mars in aphelic and perihelic opposition
See the blog about the opposition, including pictures of how small/dim
Mars looks like on the sky at conjunction vs. opposition.
Compute the ratio of brightness (i.e. flux of radiation received)
and express as magnitude difference. As in the first problem,
Earth's orbit can be assumed circular.
SOLUTION
As with all the problems involving illumination, brightness and (later in the
course) temperature calculations, we first mentally draw a sphere surrounding
the source of radiation (sun) wit radius equal to the distance to illuminated
body (Mars). The bolometric (all-wavelengths) flux of energy is solar
luminosity $L_\odot$ spread evenly on that imaginary sphere, so flux of solar
radiation at Mars, $F$, diring its aphelion/perihelion, is
$$F_{a,p} = \frac{L_\odot}{4\pi a_M^2 (1\pm e_M)^2}. $$
That needs to be multiplied by the cross section of Mars and by a constant
describig how well Mars scatters radiation (to be later received on Earth)
-- we call it albedo. But these things are all constant, the same at (a,p)
points, so they'll not be important for the ratio of fluxes below.
Next, light scattered off Mars has to get to Earth, so we mentally
distribute the scattered power on a big sphere with radius $d_{a,p}$
and area $4\pi d^2_{a,p}$, where expressions for $d^2_{a,p}$ have been
derived in the previous problem.
Finally, we divide the two fluxes received on Earth to get their ratio (many
constants cancel and will not be important for the result):
$$ \frac{I_p}{I_a} = \left[\frac{ (1+e_M)(a_M(1+e_M) - a_E) }
{ (1-e_M)(a_M(1- e_M)-a_E) }\right]^2 \,.$$
Units check out ok, and the ratio evaluates to 4.43, i.e. at the next
perihelic opposition Mars should be as much as 4.43x brighter than at the
present maximum (about -1.65 magnitudo in astronomical, logarithmic scale
$\Delta m = -2.5\log I_p/I_a$). This difference in brightness is totally due
to Mar's orbiotal eccentricity.
Time span from aphelion
around now to perihelion is half its orbital period or 687/2 days, but then
Mars won't be in opposition! Oppositions happen every 780 days, so you can do
the math of when we will see the next perihelic rather than aphelic
opposition.. or, if you want, you can ask google, exceptionally!
It's in Sept 2035. Go out on a clear night, find Mars in Gemini constellation
to the east of Orion, it's a visibly reddish 'star' as bright as the
nearby Sirius in Canes Venatici constellation (Hunting Dogs of hunter
Orion). Remember how it looks, to tell your friends in 2035 that you are
following Mars since its oppositions were bright but not SO bright.
We also started discussing the comet Dibiasky from the movie, but didn't get
far. See below.
Tutorial 2 on 23 Jan 2025
Lectures: Strange results of explosion in space, and 2
descriptions of ellipse
During the lectures,
we discussed a strange consequence of the fact that both the energy and the
orbital period of elliptic orbit depend only on $a$ (half-diameter of orbit),
and not on $e$ (its shape)

Imagine an explosion in empty space of an object that spreads debris in
every direction with equal speed $v$ from some point X. If there are no other
particles in the universe, then the debris will never return, but if there is
a point mass M at distane $r$ from X, and if $v$ is less than the escape speed
from M at distance $r$, the mass will focus the debris into elliptic orbits
having the same $a$ and $period$ P, and different shapes, described
by various eccentricities $e$. So the explosion will sort-of be reversed,
and all the debris particles will come back to point X in time P!
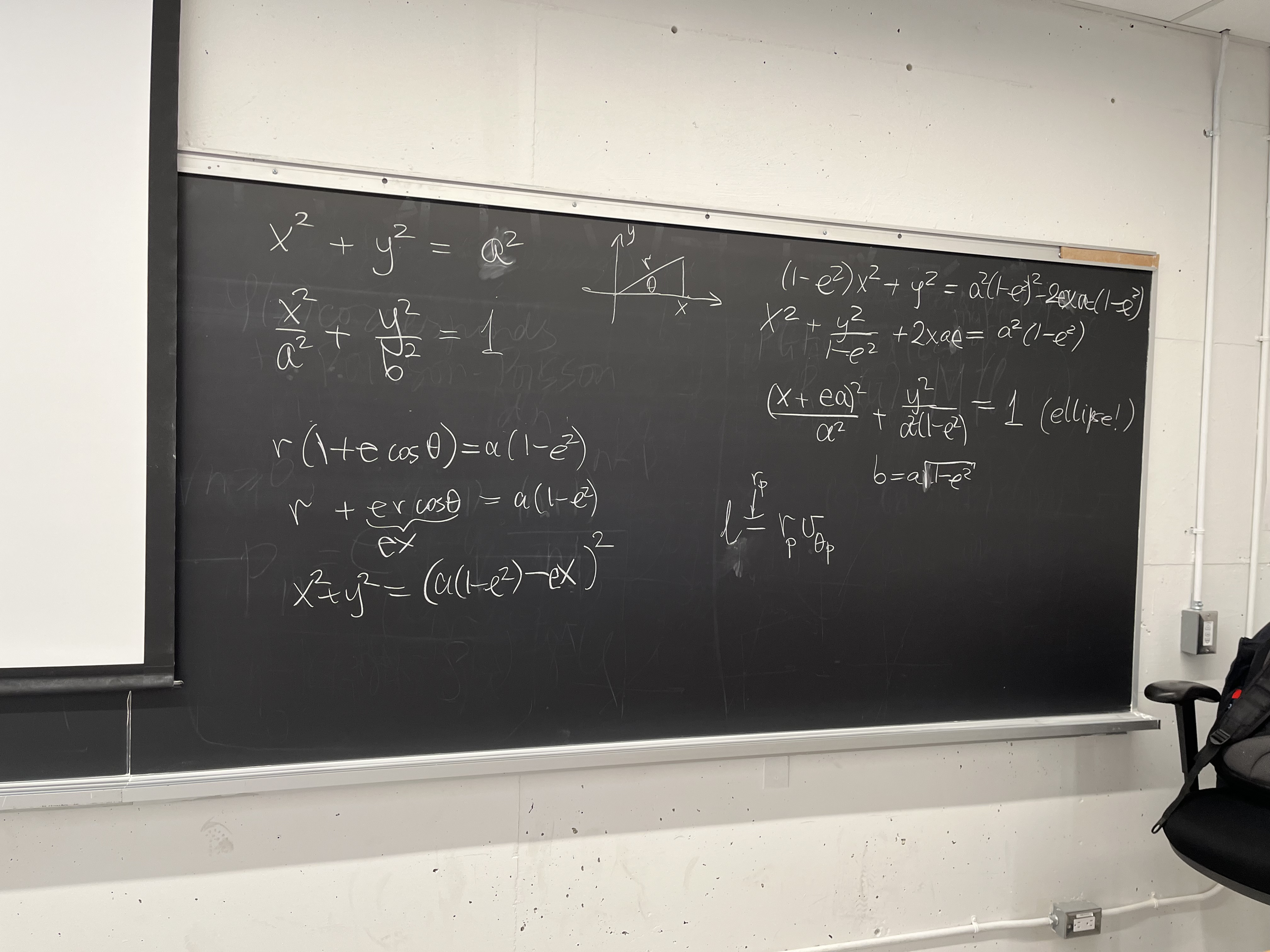
Above is the proof from the lecture that the polar-coordinate ($r,\theta$)
version of the equation of ellipse: $r(\theta) = a(1-e^2) /(1+e \cos \theta)$,
is identical with the more familiar Cartesian version of ellipse as a circle of
radius $a$ (equation $x^2+y^2=a^2$), contracted by a factor $b/a$ along
y-direction: $$\frac{x^2}{a^2} + \frac{y^2}{b^2} =1. $$
The proof furnishes the aspect ratio as a function of eccentricity $e$ in the
form $b = a \sqrt{1-e^2}$, which is equivalent to fact that the sum of distances
from two focal points of ellipse to every point on the curve is constant and
equal $2a$, as we have figured out in T1.
Impact: Comet Dibiasky
The comet may be fictitious (cf. 2021 movie "Dont't look up") but the problem is
real and applies to comets that have hit the Earth in the past. They come
from Oort cloud, their aphelia are from 10$^3$ to $10^5$ AU from us.
Assume inclination of the orbit $i=90^\circ$, aphelion at $r_a = 10^4$ AU, and
perihelion at $r_p = 1 $ AU. We actually could assume a smaller perihelion
distance, and the results would be practically identical, but it is easiest to
take $r_p=1$ AU.
Use the laws of elliptic motion (see the introduction to assignment set A1).
Derive $a$ and $e$ of the orbit, and perihelion velocity $v_p$, neglecting
the presence of Earth. Then find the way to take into account an increase of
the velocity by the time of impact, due to gravity of Earth.
In the end, find the impact speed by considering the perpendicular velocities
of the Earth $v_E = 30$ km/s, and $v_p$. Express the results in km/s.
Use L-conservation or E-conservation law to find the answers.
SOLUTION
This blackboard
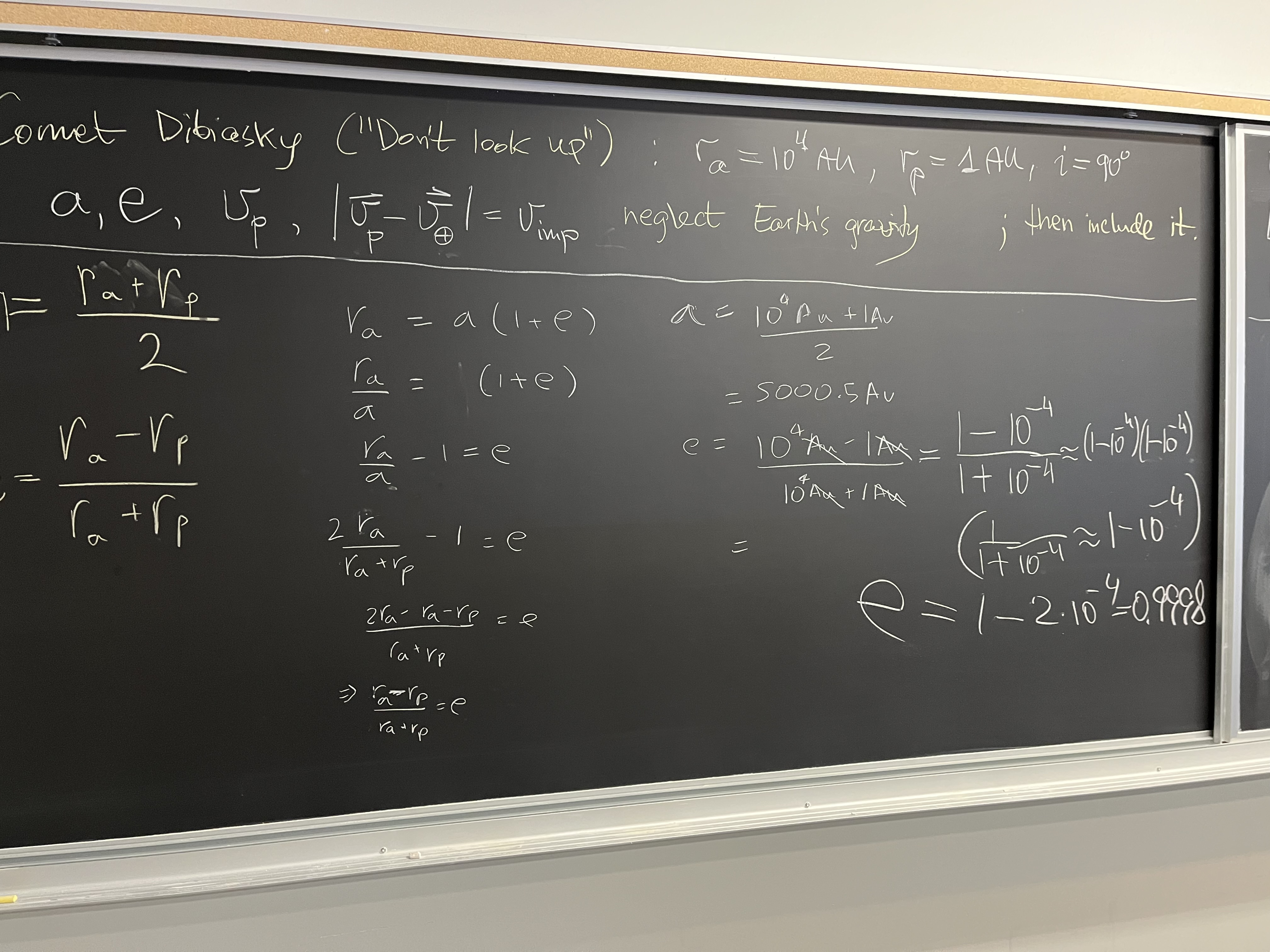
explains how to find $a$ and $e$ from $r_p$ and $e_a$. And these
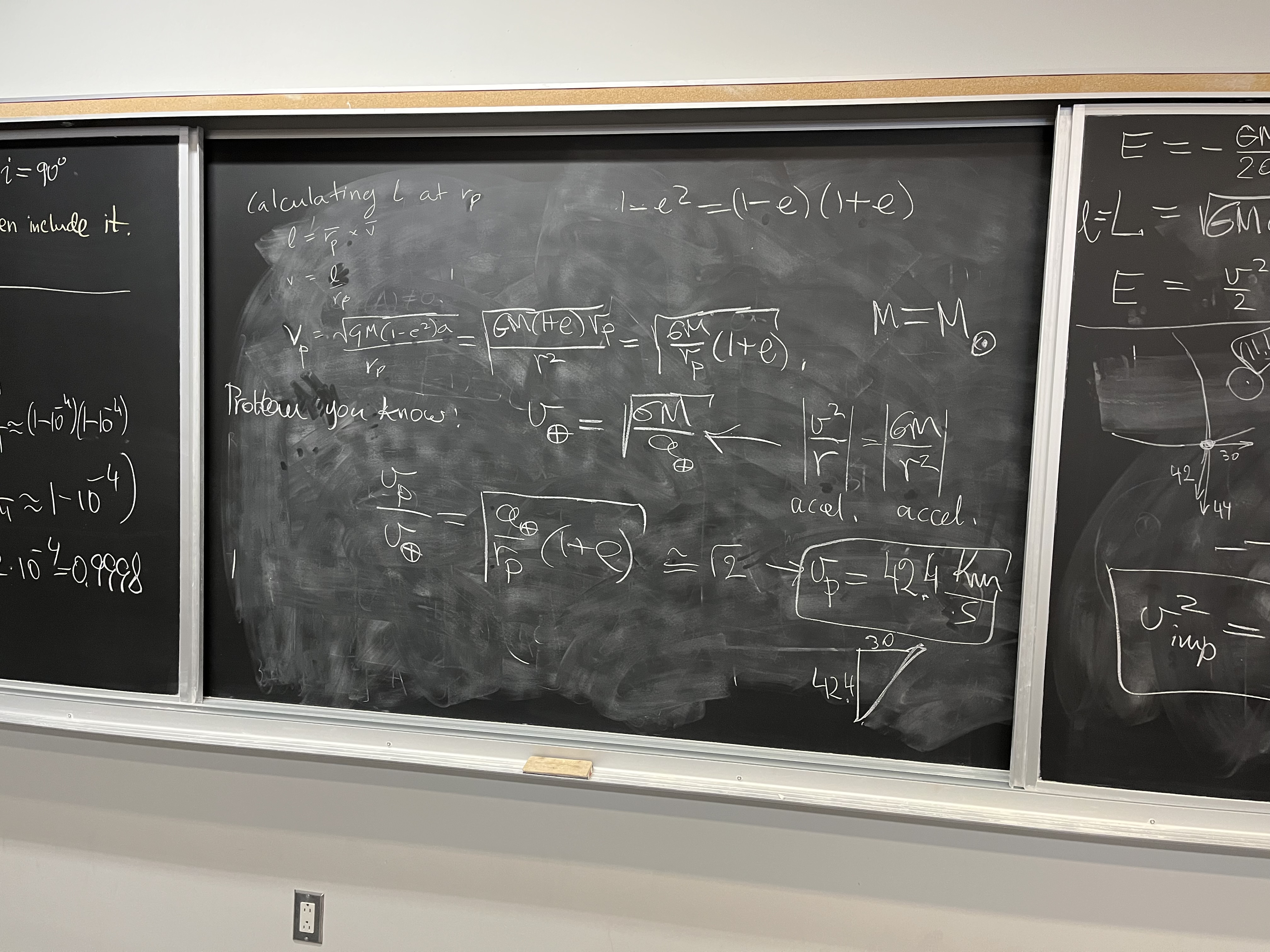
explain how to find $v_p$. This can be done in a two-step way described
in the text of the problem above. Formulae we find depend on $e$,
which is $e=1-2\cdot 10^{-4}$, very close to $e=1$, and can be replaced with 1.
(This is equivalent to saying that the comet came not from Oort cloud but
from infinity, with initial zero speed. It's a very accurate approximation to
truth. It also means that the extremely elongated elliptic trajectory inside the
solar system is almost indistinguishable from parabola.)
The comet gains kinetic energy because it sinks gradually deeper into 2
potential wells, the main one of the sun's gravity and a smaller one of Earth's
gravity. On contact with Earth, the depths (per unit mass of comet as test
particle) are $-GM/a_E$ and $-GM_E/R_E$, correspondingly. You should check the
units, they're ok. Here, $a_E = 1$ AU, and $R_E$ is the radius of the Earth.
So, in inertial frame, and multiplying both sides of equation by 2, two times
the comet's (specific) kinetic energy reaches value
$$ v^2 = \frac{2G M_\odot}{a_E}+\frac{2GM_E}{R_E}.$$
We can phrase this as follows: in inertial frame, comet's speed at impact is the
quadratic sum of the escape speeds from the sun and from the surface of the
planet. Numerically, we found that the escape speed from the sun
at 1 AU distance is 42.4 km/s, and I claim that the escape speed from Earth
is 11.1 km/s (which can be verified either by plugging in the constants and
using calculator, or by multiplying near-Earth circular speed 7.9 km/s by
$\sqrt{2}$. Thus
$$v = \sqrt{42.4^2+11.2^2}\;\mbox{km/s} = 43.8 \;\mbox{km/s}.$$
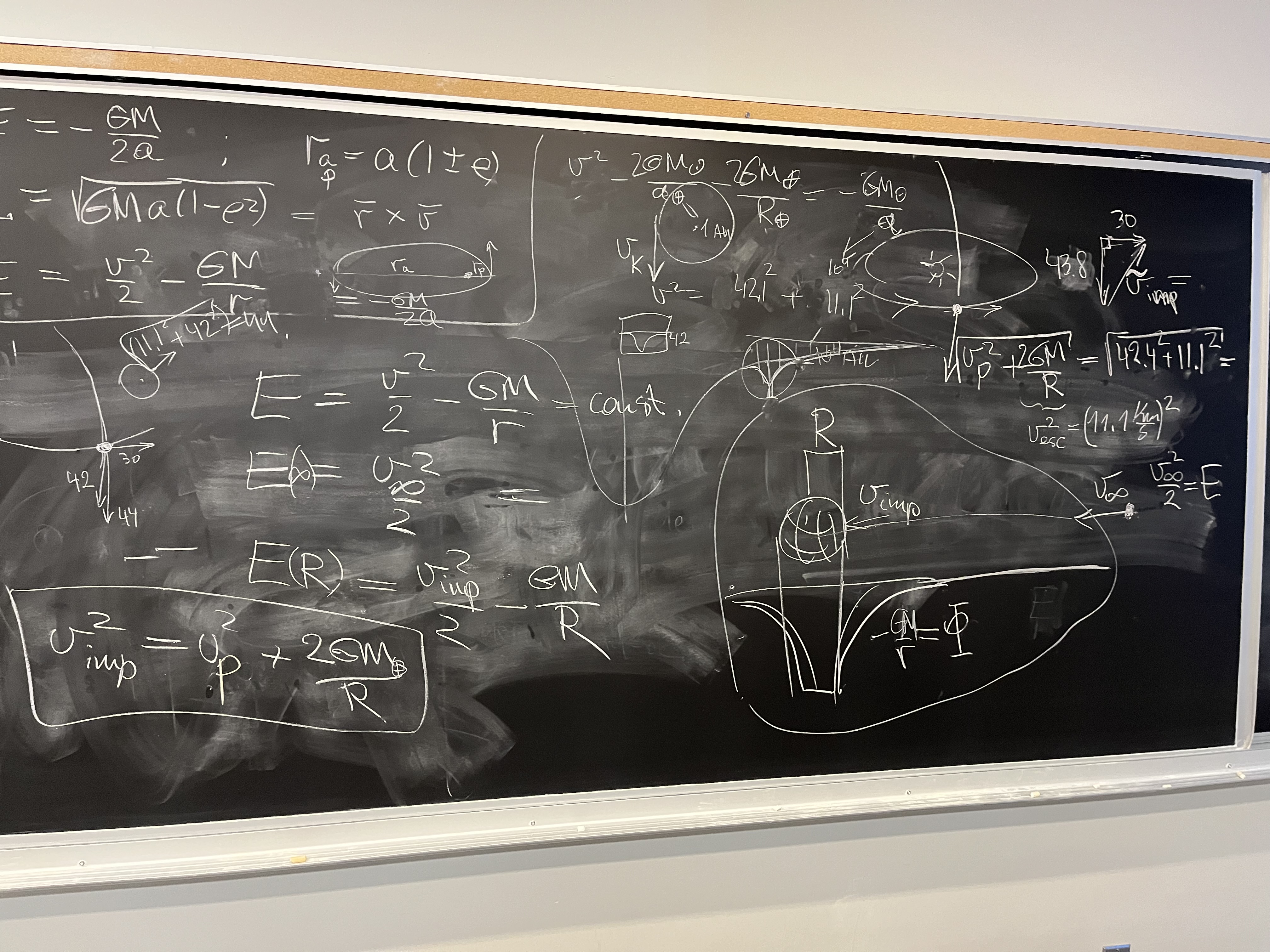
The speeds are in the inertial frame of the sun. Now we need to shift into the
moving Earth's frame of reference, to obtain the impact speed. Subtracting
two perpendicular vectors, one of the Earth's motion in inertial frame
(at 30 km/s or more precisely 29.78 km/s), and the other of the vertical motion
of the comet having speed $v$, will accomplish that. The result is this
impact speed
$$v_{imp} = \sqrt{42.4^2+11.1^2+29.78^2}\;\mbox{km/s} = 53.0\;\mbox{km/s}.$$
We will deal with the consequences of such a fast impact next time.
Tutorial 3 on 30 Jan 2025
We have reviewed all the
solutions to A1 . After that, we solved the
Energetics of cometary impact
Consider comet Dibiasky from T2. Estimate its mass $m$ by assuming a spherical
shape with 9 km diameter and a typical, fairly low, cometary
density of $\rho=1100$ kg/m$^3$ (1.1 times water density).
Convert the kinetic energy to units of the most powerful thermonuclear weapon
(Tsar Bomba, equiv. 50 Mtons of TNT) that released 2e17 J of energy (200 PJ).
SOLUTION
We know the impact speed, it's 53 km/s. The mass can be estimated as
volume ($4\pi /3) R^3 \sim 4R^3$, where $R=4.5e3$ m, so about 3.6e11 m$^3$)
times the density 1.1e3 kg/m$^3$, comet's mass is thus about 4e14 kg.
$$ E_K \approx 4e14 \; (53e3)^2/2 \sim 0.5e24\; {\mbox{J}}$$
This is $0.5e24 / 2e17 ~ 2.5 $ million Tsar Bomb energies.
That's the number of thermeonuclear bombs each of which can evaporate or
otherwise destroy a major city, and I don't know if there are even 1000 of
them on our planet (there could be 2.5 million small towns and villages,
though).
Energetics of asteroid impact
Asteroid impact has pretty much the same consequences as cometary impact.
Impact speeds are a little slower but density of impactors higher.
Please read up on one asteroidal collision
(Chicxulub event)
that wiped out 3/4 of plant and animal species 66 mln years ago
[66043000 ± 43000 years ago).
General knowledge about Chicxulub event is required -
wiki article is an extra reading assignment included in A2, and a
quiz question about it may pop up on exams. Of course, don't
pay attention to details such as which company found which rocks,
concentrate on astrophysical aspects.
A quarter of a much smaller
Meteor Crater
near Winslow, Arizona, is seen here from a low-flying airplane
(click to blow up, pun intended)

The crater is circular and has ~1 km diameter. A stony-iron meteorite,
60 m across, fell 50k yr ago with an estimated impact speed 20 km/s.
In 2024, With one u/g student from DPES we hiked uphill to the rim
of the crater from the south. We did not descend into the crater. It was an
unofficial exploration, ignoring 'No tresspassing. Terrain monitored" signs.
(The crater is privately owned.) Estimate the kinetic energy in J, show that
it was equivalent to 100 Mt TNT, 2 or 3 times higher than the Tsar Bomba.
Additional question, appropriate for introductory Physics course: If an
airplane flies just inside the crater's rim at constant altitude & constant
speed $v=$ 60 m/s = 216 km/h = 117 kt, at what bank angle does it fly and
how many g's does the passenger feel?
Optional exercise - do if you are interested
Consider a realistic example of comet 55P/Tempel-Tuttle (55th periodic comet
discovered, which swings by the Earth's orbit every 33 years, leaving a
trail of stones along its orbit that we see on Earth as Leonid meteor shower
every November). It can come as close as 0.008 AU to Earth on its current
orbit, but what of the orbit changes slowly in time?
Find all the details of the hypothetical impact, assuming coplanar,
counter-rotating heliocentric motion of Tempel-Tuttle (its inclination is
161.57 degrees, so almost 180 degrees).
Calculate the position and velocity of the comet and Earth at impact.
Estimate mass, kinetic energy in joules. How many Tsar Bomba's is that?
Is the cometary impact an extinction-class event?
Tutorial 4 on 6 Feb 2025
Triangular Lagrange points L4 and L5
Prove that triangular Lagrange point L4 is an equilibrium point in a frame
rotating with the system of two massive bodies, in the circular, restricted
3-Body problem.
The equation of motion in rotating frame contains two gravitational attractions
from massive bodies 1 and 2, centrifugal force and the Coriolis force. But
Coriolis force in this problem is zero, since the test particle is at rest.
We have shown that for any mass parameter $\mu = m_2/(m_1+m_2)$
the equilateral triangular position has sum of 3 accelerations equal to zero.
Look at the top of this page for the schematic drawing of the R3B situation
and the proof
 which was also done by you on the blackboard
which was also done by you on the blackboard

Roche lobe radius
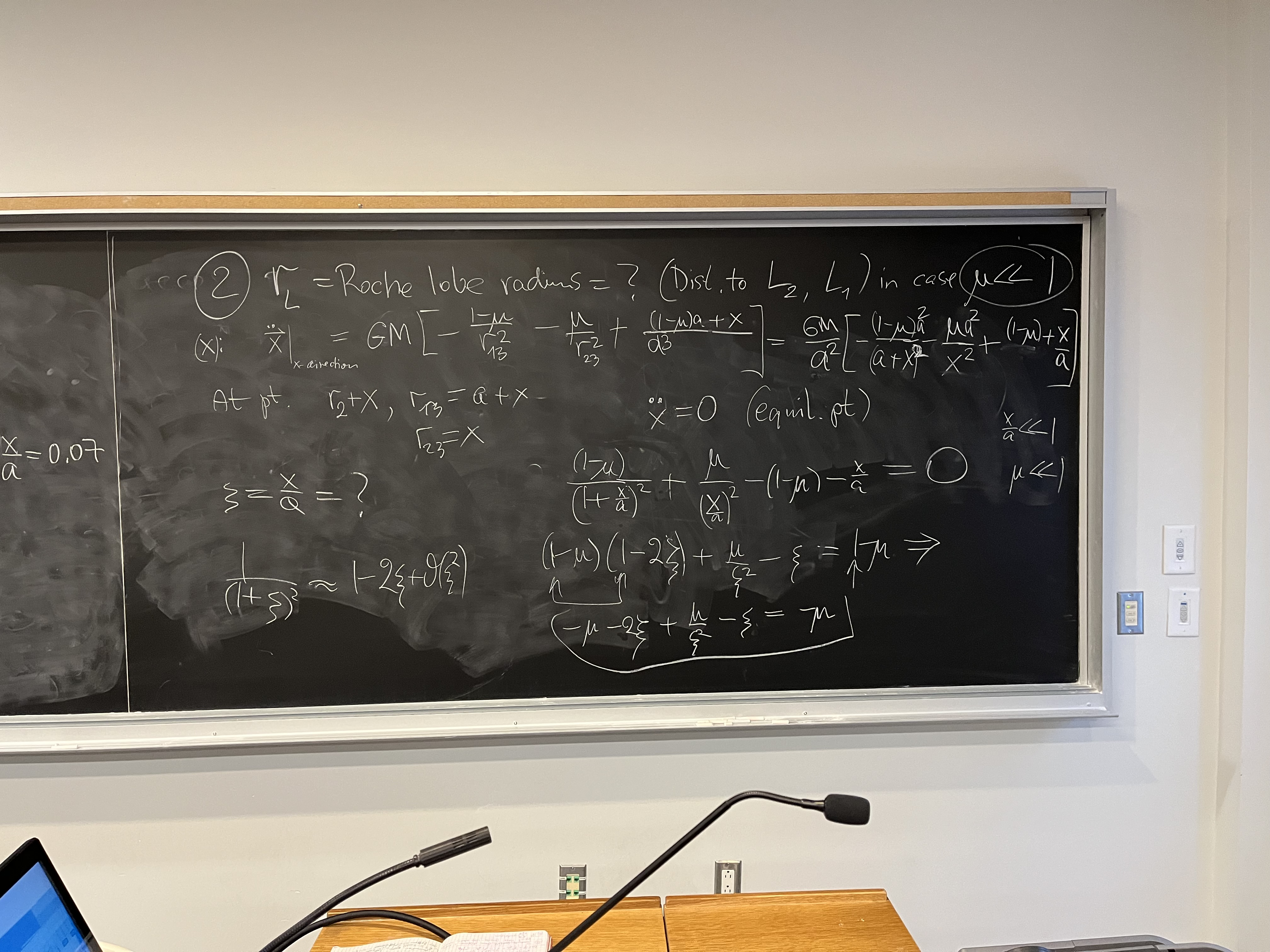
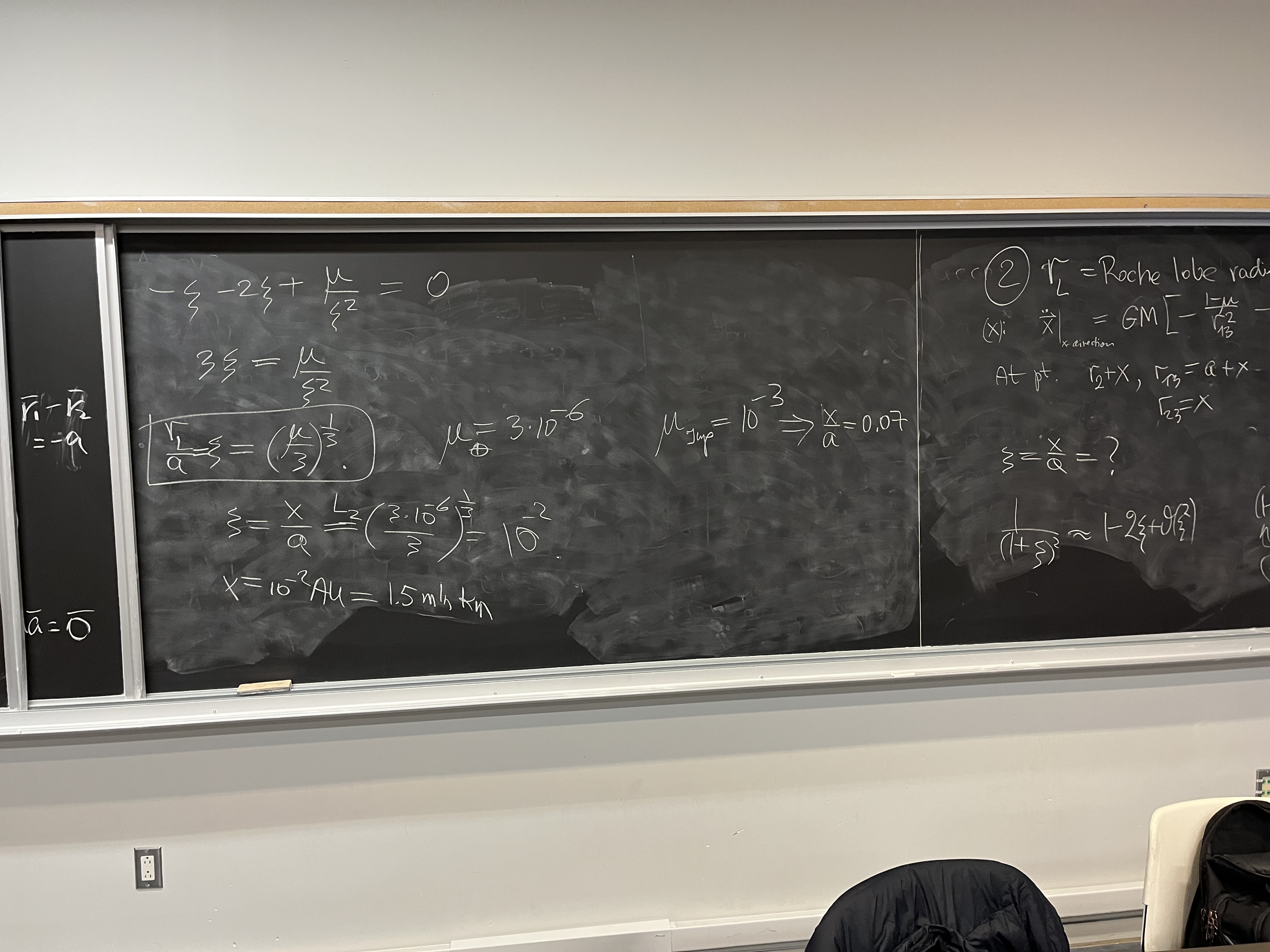
This picture generalizes our calculation from the tutorial to both L2 ans L1
Lagrange points. In the limit of very small $\mu$, both distances are
$r_L = (\mu/3)^{1/3}\,a$, so we call both of them the Roche lobe radius
(look at the bottom part):

Tutorial 5 on 13 Feb 2025
We reviewed the posted solutions to all assignments A2.
We also looked through the solutions to midterm 2024 (also posted).
Tutorial 6 - midterm
Tutorial 7 on 6 March
Time of visibility of the ISS (International Space Station)
First, we calculate the distance to horizon from the top of a tower of height
$h$.
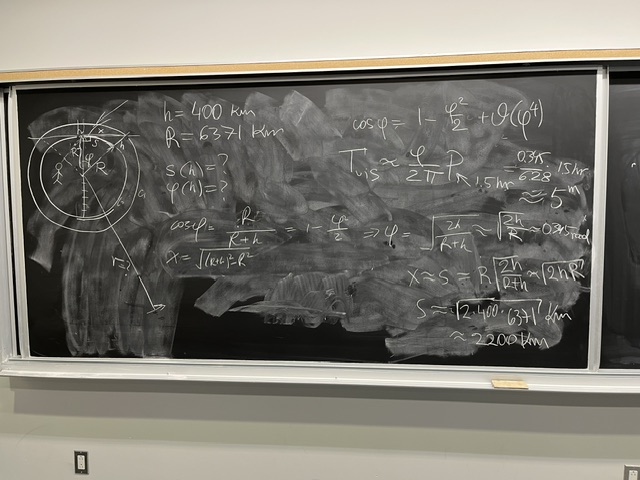
The formula says $s \approx x = \sqrt{2 h R}$. It is a remarkable formula,
because it says the climbing up the tower 100 times higher, you gain only 10
times further view. Conversely, even a small hill gives you a very good
visibility, something used by soldiers from times immemorial. For instance,
from the restaurant in Toronto's CN Tower (height about 350 m), use should be
able to see the horizon at the distance of 67 km. From 400 km orbit of ISS,
you see out to 2260 km. That's 0.0564 of the circumference of Earth (40000
km by definition).
Next, the orbital period of ISS is roughly 90 minutes, so the visibility
should last 2*0.0544*90 min = 10 minutes, if indeed we could see ISS from
rise to setting time, which is hardly possible due to clouds, haze, trajectory
not passing through zenith, and the unavoidable hills and obstacles. Notice
that you gave me time which is 1/2 of the correct time. In practice, you might
be lucky to see ISS for 5 minutes. There are sites that will tell you when and
where to look, from a given city.
How far from Earth's center and surface to a geostationary orbit?
Calculate the value ab initio. Googling the answer, as always, is allowed only
as a verification, after you've solved the problem yourself from the first
principles (or 'ab initio' in Latin, meaning 'from the beginnings').
SOLUTION
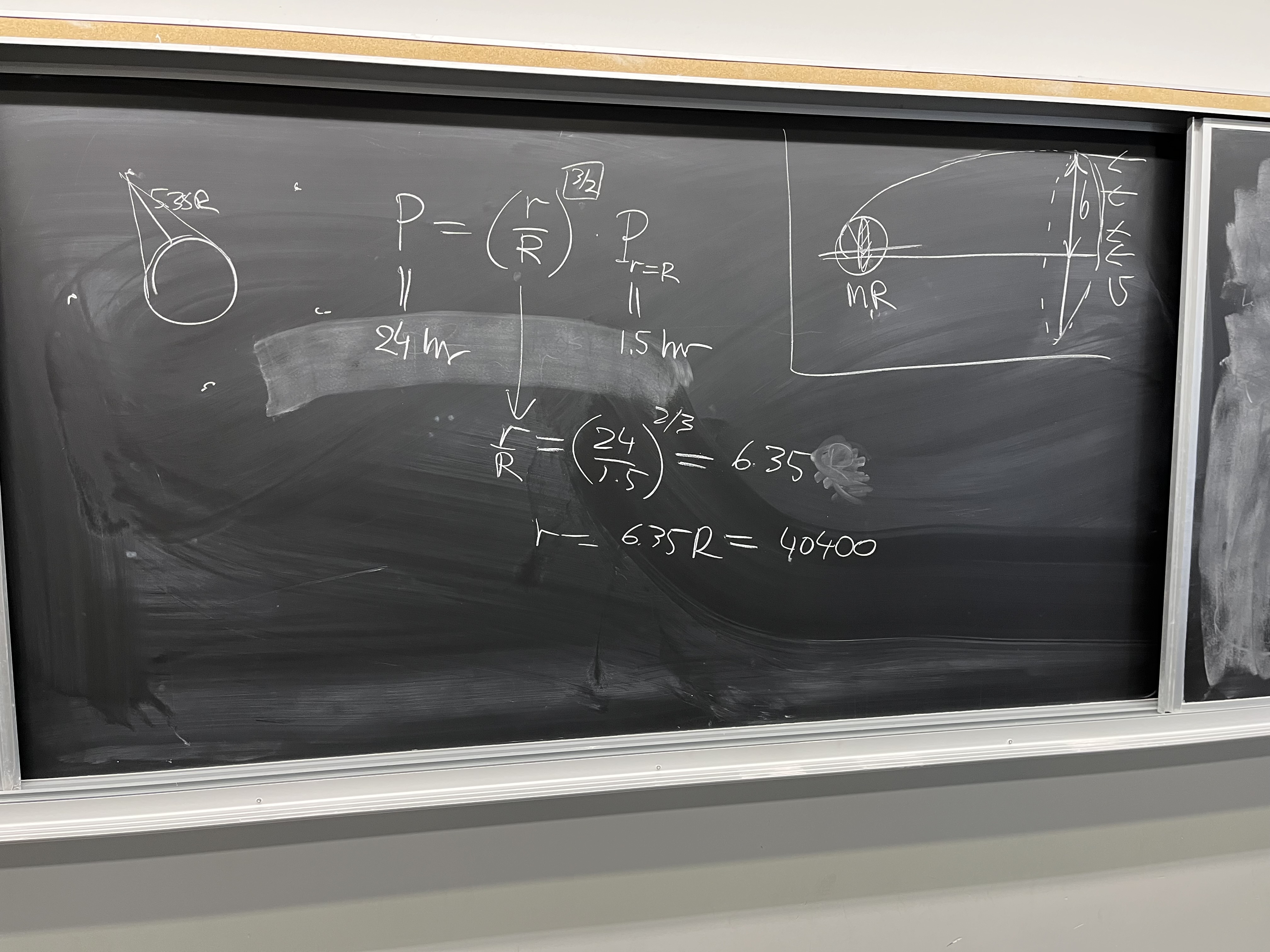 Ans: 6.35 Earth radii from the center, 5.35 from surface (about 36000 km).
At the speed of light, you can send+receive the signal to+from a geostationary
communications satellite in about 0.2s, if it answers instantaneously.
So you can talk with between different, nearby, continents with a small delay.
Ans: 6.35 Earth radii from the center, 5.35 from surface (about 36000 km).
At the speed of light, you can send+receive the signal to+from a geostationary
communications satellite in about 0.2s, if it answers instantaneously.
So you can talk with between different, nearby, continents with a small delay.
Focusing factor
As a preparation for finding the average number of comets ejected from
a planetary system, derive the focusing factor $b/R$. The picture above
(upper right corner) explains what the symbols mean.
Solution will be reviewed next time.
Tutorial 8 on 13 March
Calculate $\beta$ using geometrical optics
As long as the radius $s$ of a body scattering and/or absorbing light of
wavelegth $\lambda$ satisfies $s \gg \lambda$, you can use geometrical optics
of light rays.
Consider black-body particles (no scattering, just absorption)
of physical density $2\times $ water (2000 kg/m$^3$), having the shape of
a sphere of radius $s$. Derive the radiation pressure coefficient $\beta =
|F_{rad}/F_{grav}|$.
SOLUTION
On the blackboard, I lost $c$, the speed of light, after the first few equalities..
it should be in every denominator!
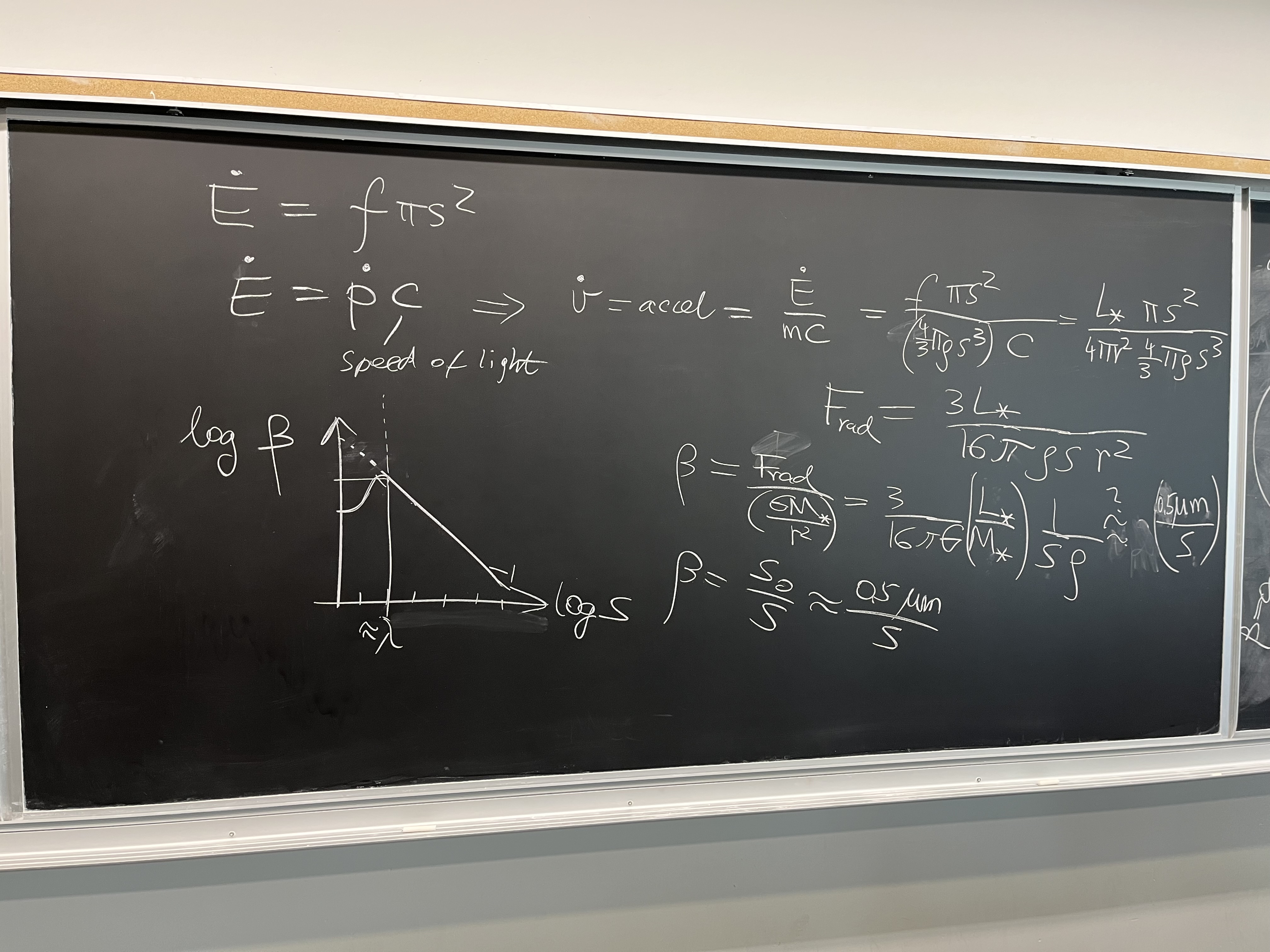 $$ \beta = \frac{s_0}{s}$$
where
$$ s_0 = \frac{3}{16\pi G c\rho} \left(\frac{L_*}{M_*}\right).$$
Check the units. They are OK. Substituting the values of constants, we get
$s_0 = 0.28\, \mu$m (it's a fine dust size). Also, its less than a peak
wavelength of solar light $\lambda \approx 0.4\mu$m. So the geometrical optics
cannot really tell us what happens when $s=s_0$. Which doesn't mean that there
is something wrong with the formula. We simply should not use it for
$s < 0.5\,\mu$m. Within the domain of applicability of geom. optics,
radiation pressure rises to just above 0.5 of gravity.
$$ \beta = \frac{s_0}{s}$$
where
$$ s_0 = \frac{3}{16\pi G c\rho} \left(\frac{L_*}{M_*}\right).$$
Check the units. They are OK. Substituting the values of constants, we get
$s_0 = 0.28\, \mu$m (it's a fine dust size). Also, its less than a peak
wavelength of solar light $\lambda \approx 0.4\mu$m. So the geometrical optics
cannot really tell us what happens when $s=s_0$. Which doesn't mean that there
is something wrong with the formula. We simply should not use it for
$s < 0.5\,\mu$m. Within the domain of applicability of geom. optics,
radiation pressure rises to just above 0.5 of gravity.
Below the size $s\approx \lambda$ (wavelength of light), the wave
optics applies, and results in a certain decrease of radiation presssure
coefficient $\beta$, like in the log-log plot provided. But that's outside
of our scope here. Let's just say that we're not interested in
$s \lt \lambda \approx 0.5\mu$m.
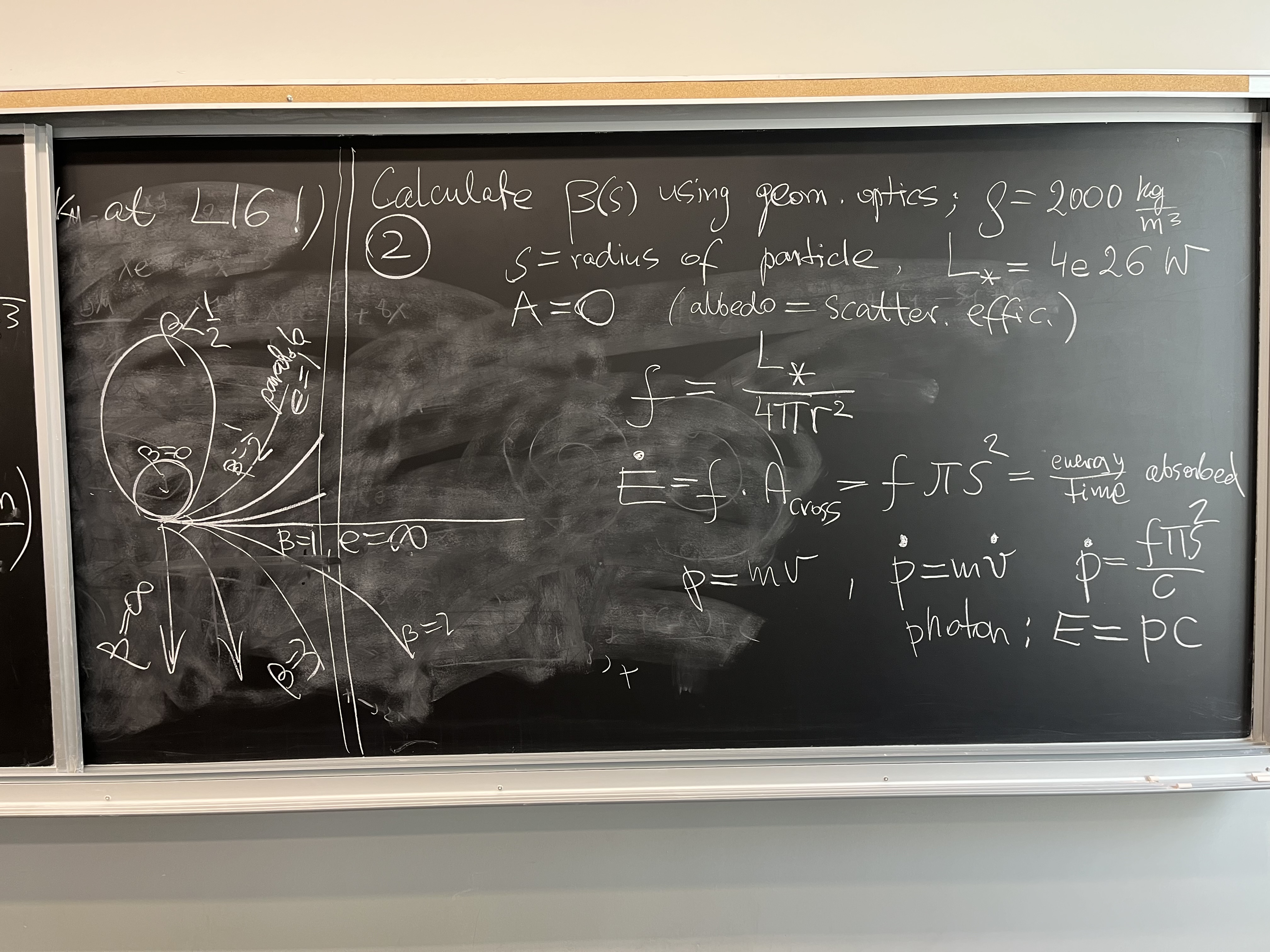 Formula $\dot{E} = f \pi s^2$ is the usual
calculation of energy deposition rate, and $\dot{E} = \dot{p}\, c$ is the
relationship of photon's energy and momentum ($\dot{p} = m\,\dot{v}$).
And $\dot{p}$ is the same as force in Newtonian dynamics.
Formula $\dot{E} = f \pi s^2$ is the usual
calculation of energy deposition rate, and $\dot{E} = \dot{p}\, c$ is the
relationship of photon's energy and momentum ($\dot{p} = m\,\dot{v}$).
And $\dot{p}$ is the same as force in Newtonian dynamics.
Don't yet pay attention to trajectories on the left, they're the solution to
the next problem.
Debris trajectory
Assume a debris particle is detached by meteor collision from its parent body,
on circular orbit around a star, which is so large that its $\beta=0$
(cf. previous problem). Suddenly, the debris particle find itself illuminated
by the star, its $\beta > 0$ (non-negligible radiation pressure coefficient),
at the distance $r$ from the star of mass $M$.
Question: What is the eccentricity $e$ of the orbit that the debris particle
enters? (In other words, derive $e(\beta)$ relationship).
If you predict that large values of eccentricity are possible, it may be
relevant to the existence of quite extended debris disks around stars:
asteroids may collide within, say, 50 AU distance, but the dust disk can
extend to 1000 AU, if $e \sim 0.9$ or more.
SOLUTION
In the tutorial, we used energy integral to derive the result.
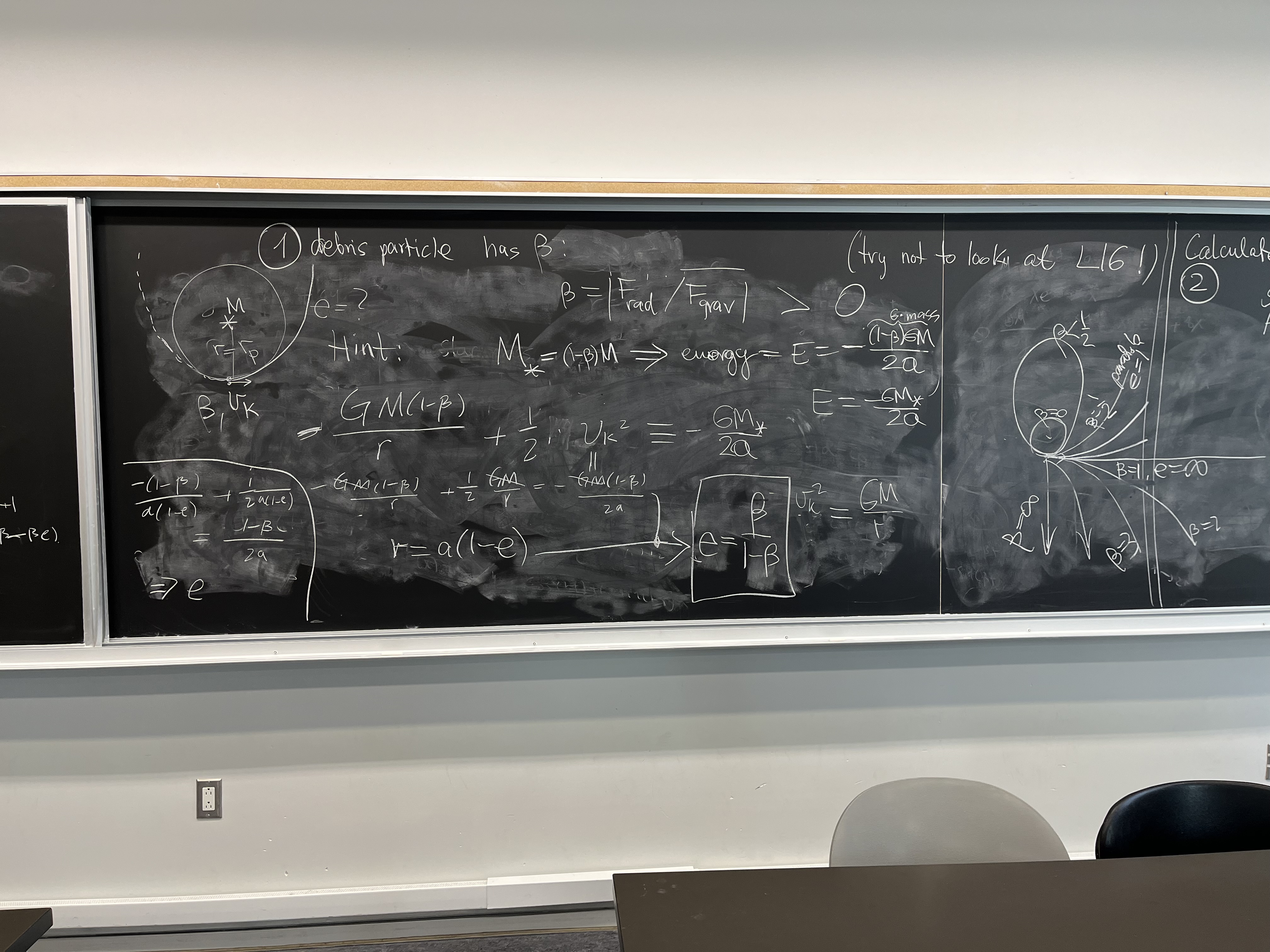
The proof goes like this:
The particle moves in two superposed force fields: one of gravity, the other
of radiation pressure. Both have the same radial dependence $r^{-2}$
on distance from the star, so there is a constant ratio $\beta$ between the
two. Potential energy being the sum of the two potentials, reads
$$-\frac{GM(1-\beta)}{r}.$$
Kinetic energy is initially $v_K^2/2 = (1/2)\,GM/r$, following from the
equality of centripetal and gravitational accelerations (radial force
balance). The total energy $E$ is constant along trajectory, since there is
no friction, and can be written at the initial point as
$$ E = -\frac{GM(1-\beta)}{r} +\frac{GM}{2r} = const.$$
For $\beta >0$, the inital point will be the closest point to the star,
a pericenter, where $r = a(1-e)$.
One the other hand, 2-body dynamics says that $E = -GM_*/(2a)$.
In our case, to take into account an effective reduction of gravity by
the opposing force of radiation pressure, we write $M_*$ (effective mass)
as $M_*= (1-\beta) M $. So the second equation for $E$ is
$E =-GM(1-\beta)/(2a)$. Comparing with the first expression for $E$, after
some algebra, we obtain
$$ e(\beta) = \frac{\beta}{1-\beta}.$$
Another way to derive the same result, even simpler, is to only consider
the constancy of specific angular momentum $L$. The addition of radiation
pressure force to the debris particle does not change its initial angular
momentum, because no non-radial forces are involved. Therefore, the initial
$L = \sqrt{GMr}$ that characterized both the parent and the debris bodies
before the onset of radiation effects, equals the angular momentum constant
at any point of the new trajectory:
$$L = \sqrt{GM_* a (1-e^2)}.$$
Notice that we did take into account radiation pressure by replacing
$M$ with $M_*= M(1-\beta)$.
Using $r = a(1-e)$ and cancelling common factor $GMa$, we get
$$ (1-\beta) (1-e^2) = 1-e,$$
or
$$ e(\beta) = \frac{\beta}{1-\beta}.$$
We notice that the debris will be an a bound, elliptic, orbit
if $\beta < 1/2$.
In particular, it will be on a circular orbit ($e=0$) if $\beta =0$.
When $\beta=1/2$, debris particle enters a parabolic escape orbit.
For larger $\beta$, as $\beta \to 1$, cf. the picture above (left side),
the hyperbola gradually becomes a straight line. This is so, because
$\beta =1$ is the case of zero net force. In that case, Galileo's law of
inertia states that the path is a line, and the velocity is constant.
For $\beta > 1$, the orbit is hyperbolic but bet away from star.
As $\beta \to \infty$, the asymptotic trajectory simply shoots out
of the point of debris creation radially, away from the star.
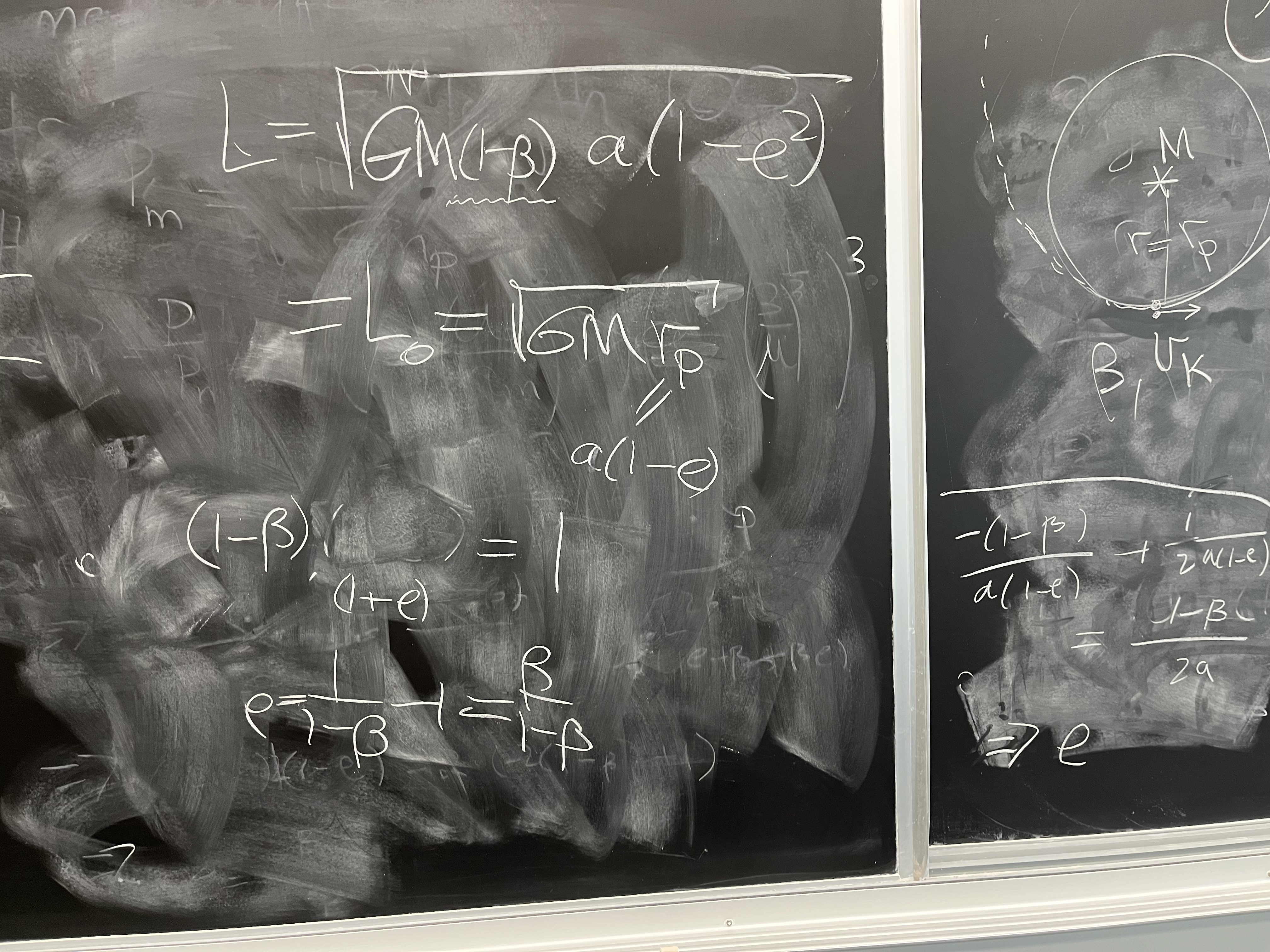
Review the solutions to A3
Yes, we've done that in the tutorial, not all problems, though.
Consult the solutions file in the usual location for details.
Tutorial 9 on 20 March
How many comets are ejected from an average planetary system?
The statistics shows that most stars have observed planetary systems, one can
even say that every star in the Galaxy has a planetary system of some kind,
not necessarily detectable one at present. On average, there are 0.15 stars per
pc$^3$ in our Galaxy, which we write as number density $n_* = 0.15/\mbox{pc}^3$.
How many planetesimals (comets, but also asteroid-type bodies)
does a planetary system eject into space?
Typical velocities of interstellar comets w.r.t. sun (at infinity) are
$v_\infty =28$ km/s. Assume that comets with perhelia out to $R=8$ AU are
detectable, and that the event rate is $\dot{N}=1/(5$yr), because in the last
decade we have seen 2 interstellar objects. Yes, the statistics is quite poor
so far, but assume for the rough estimate that 1 interstellar object is
detected every 5 years. (Future observations may change that number either
up or down.)
Hint: To be on a safe side, apply the gravitational focusing factor (a sphere
with larger than 8 AU radius is the actual effective target for straight
initial motion of the objects, because their trajectories are bent somewhat
by the attraction toward the sun.
SOLUTION
Summarizing our efforts, effective target area is $\pi b^2$, and parameter
of encounter $b$ is in a ratio with $R$ following from energy and angular
momentum conservation:
$$ \frac{b^2}{R^2} = 1 + \frac{2GM_\odot}{R v_\infty^2}. $$
We replaced $GM_\odot/R $ with $(R_{AU}/R)(GM_\odot/R_{AU}) = (1/8)(30$ km/s)$^2$
because at $R_{AU} = 1$ AU, Earth goes at the speed of whose square is
(30 km/s)$^2 = GM_\odot/R_{AU}$. That gives target area
$ b^2/R^2 = 1 + (2/8)30^2/28^2 \approx 1.28$, which isn't much; we have
honestly proven that the
gravitational enhancement of target area with
respect to the basic $\pi R^2$ is only by a factor 1.28.
The number of interstellar objects (let's call them comets) passing through
a sphere of radius $b$ per unit time is
$$ \dot{N} = n_c v_\infty (\pi b^2) = 1.28 \pi n_c v_\infty R^2$$
It does not matter from which directions those objects are coming, the
only important thing is their spatial density (number per unit volume) $n_c$
and their speed at infinity $v_\infty$. Even though every object comes
from a different direction, the cross section of an R-radius sphere that it
is aiming at is always perpendicular to the trajectory at infinity. We
turn all the incoming directions to be along x-axis in the figure on
the blackboard below (to which you astutely objected, thank you).
The number of events is just the product of $v_\infty n_c$ and the
target area, as if object were all coming from one direction.
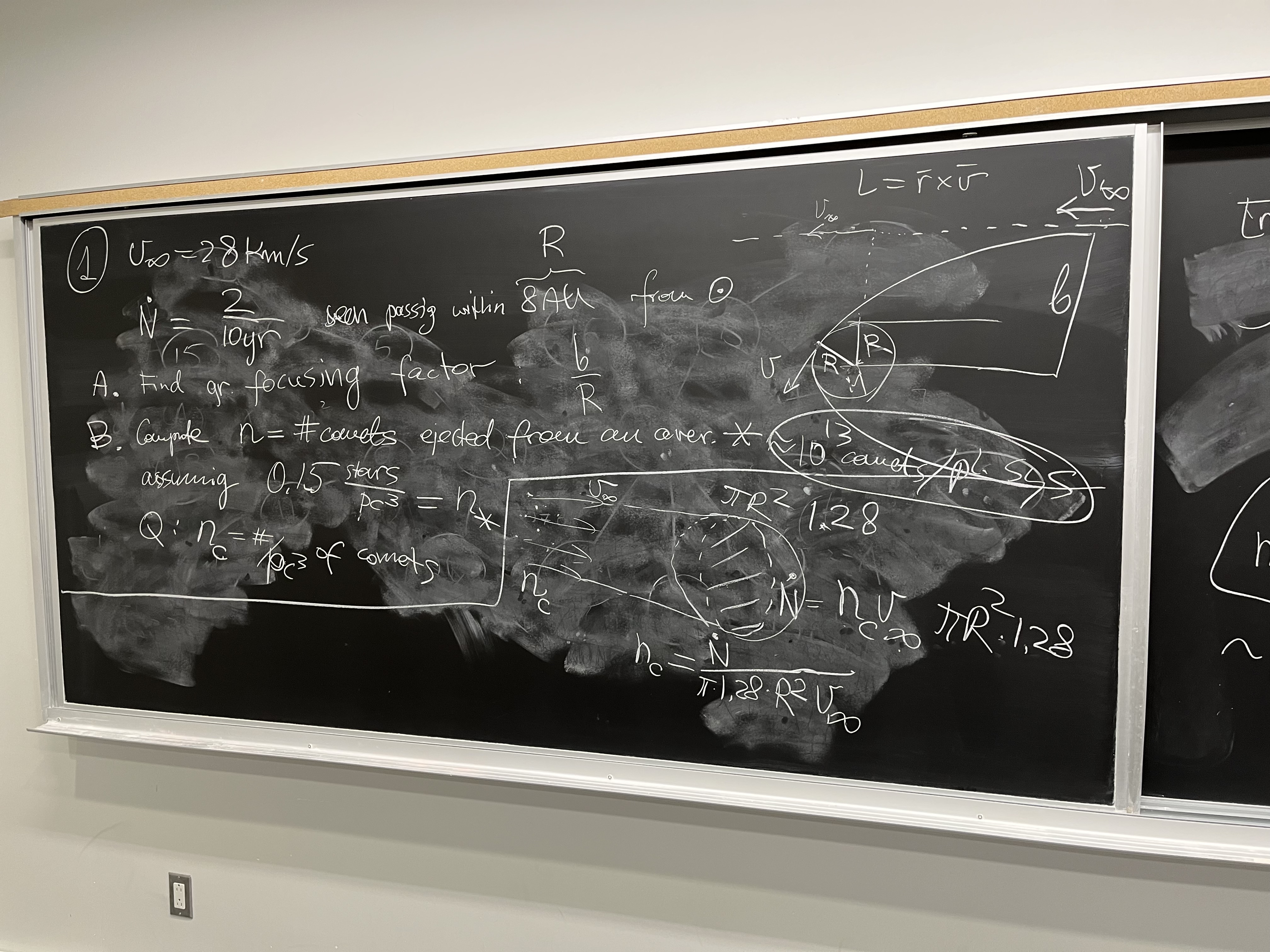
The above formula allows us to estimate $n_c$. And the number $n$ of
comets ejected by one average star (i.e. each planetary system) is the
ratio of the number density of ejected comets to the number density of
stars, counted in a volume of the Galaxy big enough for good statistics:
$$ n = \frac{n_c}{n_*} = \frac{ \dot{N} }{ 1.28\pi {v_\infty}n_* R^2}$$
Units check out (no units on either side). We plug values w/o convertig them
to S.I. No calculator will be needed.
$$ n = \frac{ \mbox{pc}^3}{ 1.28 \cdot 5 \mbox{yr}\, v_\infty \;\pi\, 0.15\cdot
8^2 \mbox{AU}^2}$$
But $v_\infty$ is 28/30 of Earth's orbital speed, so (1yr)$ v_\infty =
(28/30) 2\pi$ AU = $\pi$ (28/15) AU, using the $2\pi$ AU circumference of
Earth's orbit. We will also need to convert pc to AU: pc/AU = 206265 ~ 2e5.
$$ n = \frac{ 8 \cdot 10^{15} \mbox{AU}^3}{ 1.28 \cdot 5 (28/15) \;\pi^2 0.15
\cdot 8^2 \mbox{AU}^3} \approx \frac{10^{15}}{ 5 (28/15) 1.5 (1.28\cdot 8)}
\approx \frac{10^{15}}{5 \cdot 28} \sim 10^{13}.$$
Notice how we did not do order-of-magnitude rounding initially, and waited
with it till the last step. Namely, it happens that you round quantities
like, say, 2.9 and 2.5 both to 1 in an intermediate result, losing one order
of magnitude in their product: 2.5*2.9 $ \sim 10$.
Here on the right is our brave attempt at quick arithmetic during the
tutorial (inexplicably, I somehow got the final order of magnitude right,
despite dropping one instance of $\pi$ in the upper-right corner, and the
final embarassing step 4/1200 = 1/4, which would actually be
$\sim 1/10$!):
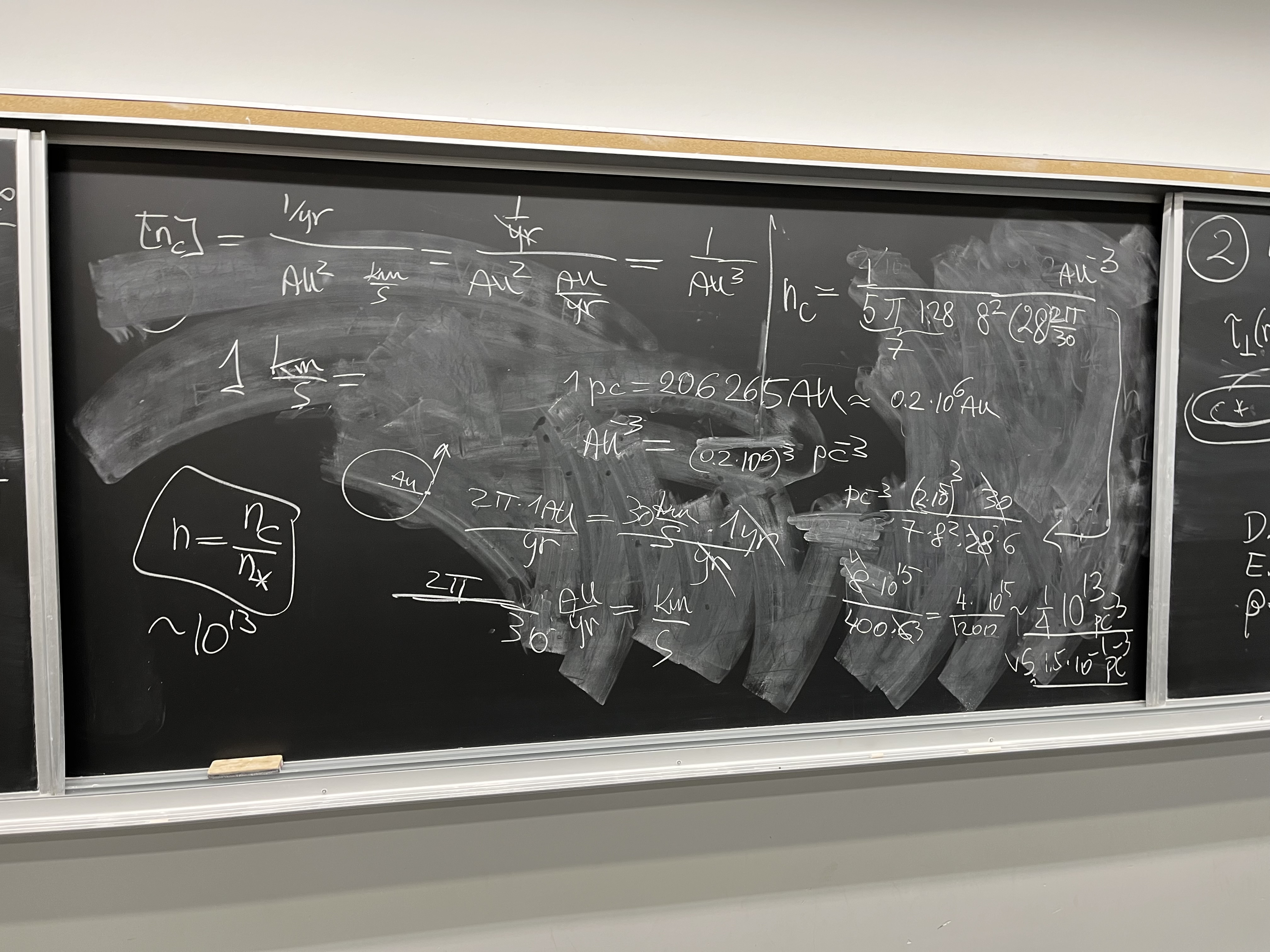
The huge number we obtained is in a good agreement with the scenario of
planetary system formation presented in lectures, where a protoplanetary
disk is able to form up to $10^{14}$ planetesimals, but the giant planets
(using up most of them for construction of the cores) can easily eject a big
part the remaining planetesimals from their vicinity to the Galaxy.
If all our numerous assumptions are true (possible, if unlikely :-),
then about 1 out of 10 small bodies that form in a protoplanetary disk is
ejected to the Galaxy, based on the theoretical number of planetesimals,
and this exercise based on empirical knowledge. I haven't checked, but
think that this ratio calculated in dynamical simulations of planetary
formation is roughly the same.
Commentary:
A good intuition (that you can support by doing actual numerical, dynamical
calculations, if you spend a month learning how to do those) says that in
addition to those that ecaped, about ten percent of $10^{13}$ actually did
not manage to escape to, but stayed in the Oort cloud, barely bound
gravitationally to the sun. That would make Oort cloud initially consist of
$10^{12}$ or a trillion, i.e. thousand billion comets. You can just call
it an astronomical number. Or economical (there is one dollar of Canada's net
national debt per one comet, securely stored in the Oort cloud).
Not all survived in Oort cloud to this day: some hit the sun (or, less likely,
a planet) and some did escape after a stellar flyby in the solar neighborhood.
Yet most of them probably remained there, because astronomers counting the
arrival of new comets (from Oort cloud) think that, indeed, Oort cloud has
about a trillion of them! (Hence: 'securely stored').
So, the seemingly completely independent numbers of arrivals from the Oort
cloud and from the Galaxy, are not unrelated after all.
Everything seems
consistent and explainable by our theories, even though we can't confirm
every number observationally (e.g. we can't see Oort cloud comets in situ,
or any of the $10^{13}n_* \sim 10^{12}$ interstellar comets in every cubic
parsec, in situ). Moreover, the numbers may be of the same order of magnitude
in all planetary systems throughout the whole universe.
Tutorial 10 on 27 March
Two ideas for the last tutorial spelled out here were made into A4 problems...
Prove that the $\beta$ Pic is a planetary system with an asteroid/Kuiper
belt
Beta Pictoris has mass $M_* = 1.75 M_\odot$, and luminosity $L=6.7 L_\odot$.
Beta Pic disk consists of blowout-size dust particles made of magnesium-rich
silicate such as enstatite; particles have albedo $A=0.4$ in the visible
wavelengths, and unit emissivity in infrared. Assume that the infrared excess
of $\beta$ Pic, which is a fraction of its emitted power $L_*$ which is
intercepted, absorbed, and re-emitted in IR by dust in a disk, equals
$I_{IR}/L_* = 0.004$. (You can shorten it to $q_{IR}=0.004$.)
Solve the problem by computing the collisional time of the particles in the
densest part of the disk, and comparing it with the age of the star (26 Myr).
Perpendicular optical thickness $\tau_\perp(r)$ can be approximated by the
function
$$ \tau_\perp = \tau_m \frac{2 x^2}{1+ x^4} $$
where $x = r/r_m$, $r_m =$ 100 AU, and $\tau_m$ is a nondimensional constant
(to be computed). To understand that function better, find where and
what maximum value does it attain.
Calculate the combined cross-sectional area and mass of the dust
particles located within 1000 AU from $\beta$ Pic
All the needed information have been provided in the problem above & the
result from previous tutorial about
$\beta = (0.28\mu$m $/s) (L_*/L_\odot)(M_\odot/M_*)$,
which will help you establish the blow-out size of dust around $\beta$ Pic.
Express your answer in intuitive units of AU$^2$ and Moon mass (7.35e22 kg,
or 1/81 of Earth mass).
SOLUTION
 This picture contains a hint on what integral to write, to express
the total IR power of thermal radiation by dust, $I_{IR}$, though it's
missing the efficiency factor $1-A$ (fraction of intercepted light
that is absorbed), where $A=0.4$ denotes albedo (fraction scattered).
It's a good start, but we'll return to the full answers - prepare and
volunteer next time!
This picture contains a hint on what integral to write, to express
the total IR power of thermal radiation by dust, $I_{IR}$, though it's
missing the efficiency factor $1-A$ (fraction of intercepted light
that is absorbed), where $A=0.4$ denotes albedo (fraction scattered).
It's a good start, but we'll return to the full answers - prepare and
volunteer next time!
In the footsteps of Aristarchus - not done
Solve the equation following from Aristarchos of Samos's drawing of the lunar
eclipse. Show that if Earth's total shadow is 2.6 times bigger than the Moon,
then the Moon is 3.6 times smaller than Earth. Then derive the distances and
sizes of the Sun and Moon in units of Earth's radius.
Average radius in elliptic motion - not done
Compute the time-average radius <r(t)> on elliptic orbit.
Is it equal to the semi-major axis? (That's what google AI said.)
How many planets are born per second in our universe, on average?
This was done with your help
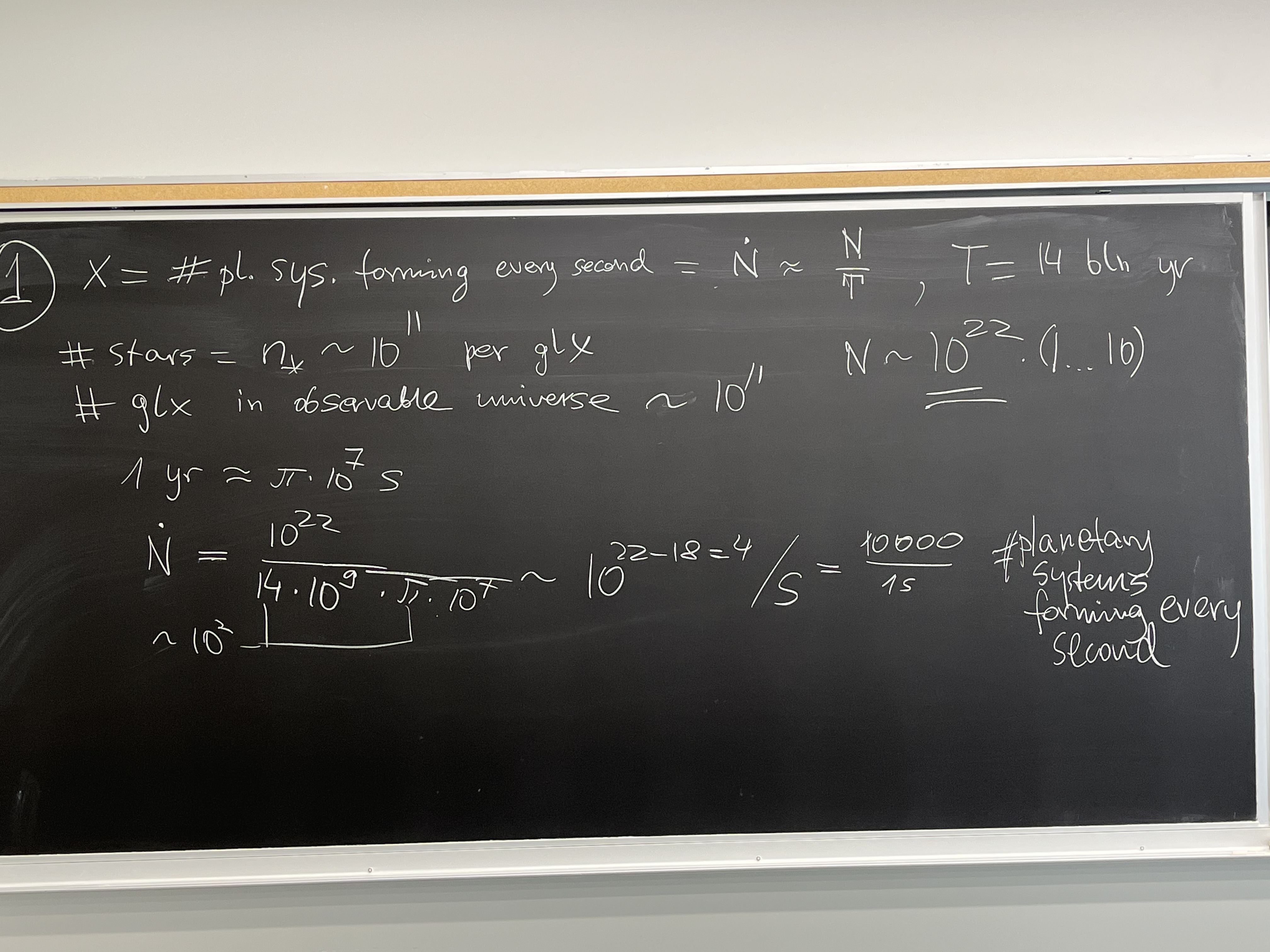
Fermi paradox NOT solved by the difficulty with travel arrangements of
Extraterrests
One of the listed reasons (see recording of this tutorial) for the Fermi paradox
is that it takes too long to travel through a galaxy, so if long distances are
involved, then we should not expect any visits from ETI civilizations in our
Galaxy.
Your task was to show that this is a wrong explanation, by first (2a) deriving
$v_\infty$ after ejection of a solar sail deliberately constructed to have
radiation pressure coefficient $\beta = 1.5$ ... 3, around a star of sun's
properties and unfurling the sail at the small distance $r_0=0.04$ AU,
and then (2b) calculating how long it takes to travel at that speed the distance
of $R_\odot = 8 $ kpc (sun-galactic center distance).
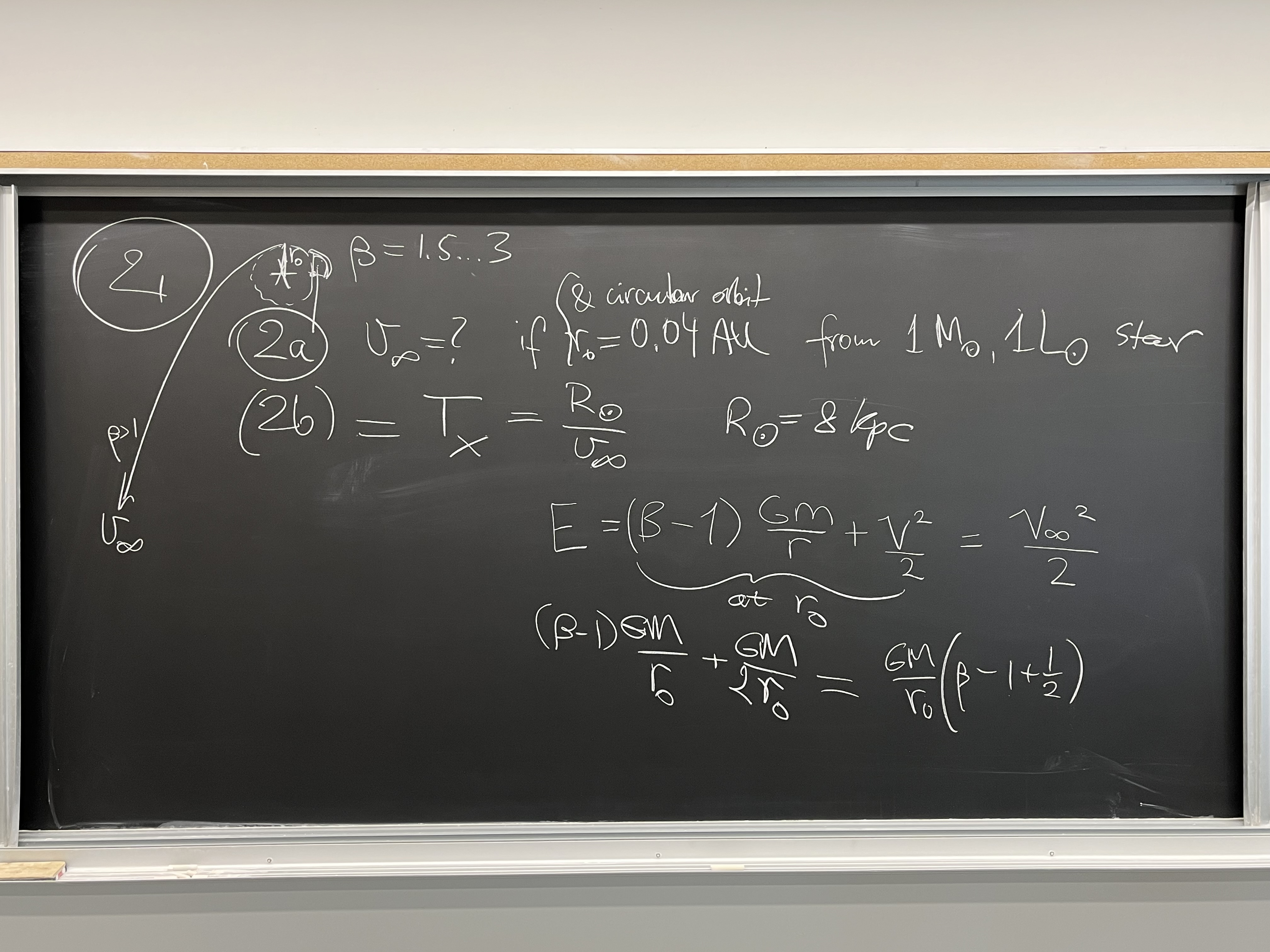
You managed to dictate a proper equation for energy conservation, and
we solved it and evaluated the answer:
$$ v_\infty = \sqrt{2\beta -1}\,\sqrt{\frac{GM}{r_0}}=(\sqrt{2} ...
\sqrt{5})\sqrt{\frac{1 \mbox{AU}}{r_0}} \;30\, \mbox{km/s}$$
Evaluation gives $v_\infty = 212$ ... 335 km/s. Being similar to or larger
than the typical linear speed of rotation of disk galaxies (Milky Way rotates
in the solar neighborhood at about 220 km/s), by appropriately directing the
flight of the solar sail against the galactic rotation, you can cancel most
of the circular galactic speed of an object, and let the apparatus plunge almost
straight toward the center of the galaxy. Or direct it some other way; in any
case the object will travel for about $T_x =R_\odot/v_\infty$ (very roughly)
until it covers about one distance between the sun and the galactic center.
This time evaluates to about 37 Myr (millions of years).
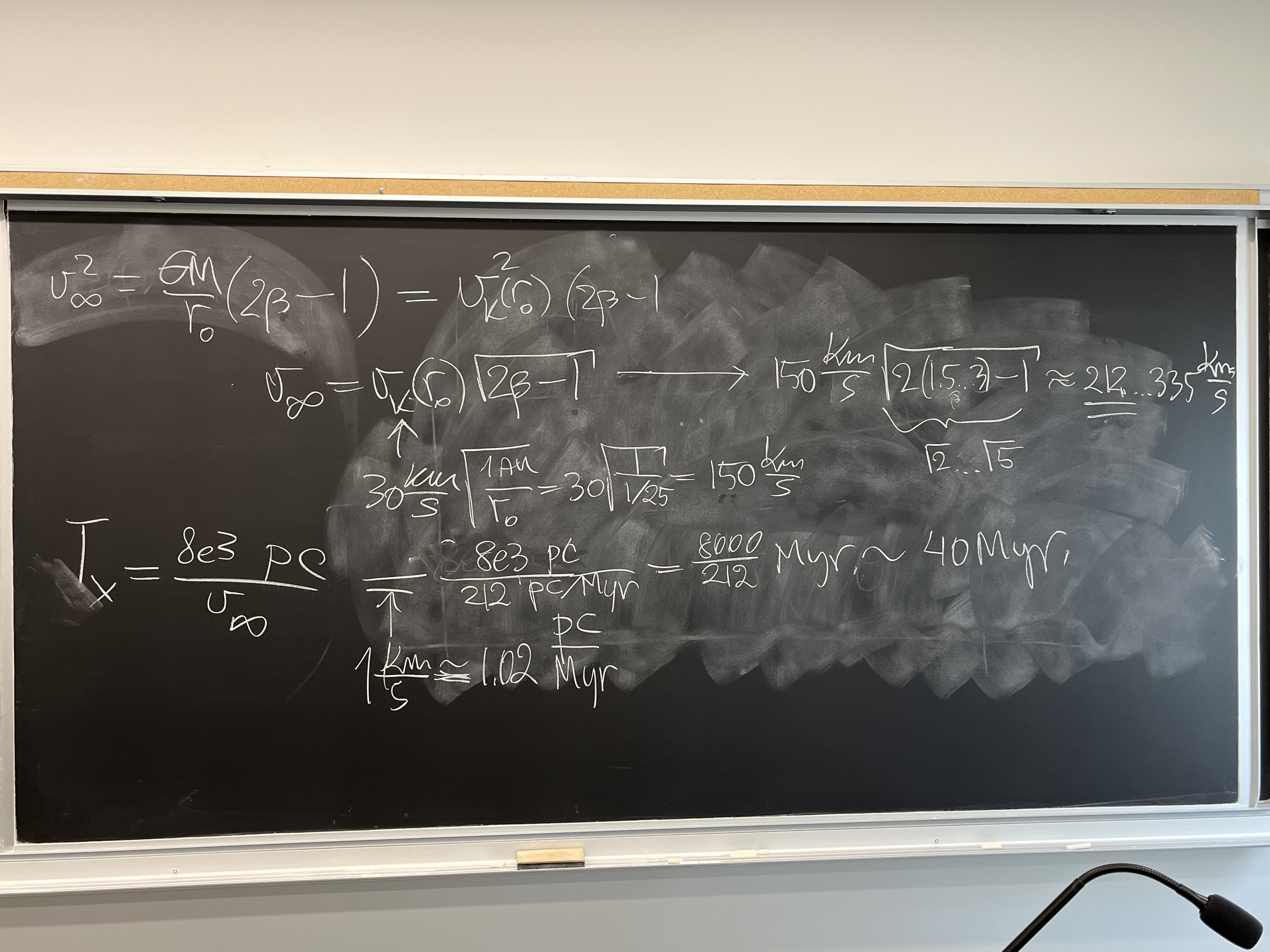 So in a life of the Galaxy and the universe, there is plenty of time to
criss-cross the Galaxy using a simple device of unfurling a solar sail near
the star. Our civilization is close to achieving the needed technology,
I believe.
So in a life of the Galaxy and the universe, there is plenty of time to
criss-cross the Galaxy using a simple device of unfurling a solar sail near
the star. Our civilization is close to achieving the needed technology,
I believe.
Coorbital satellites Janus and Epimethus
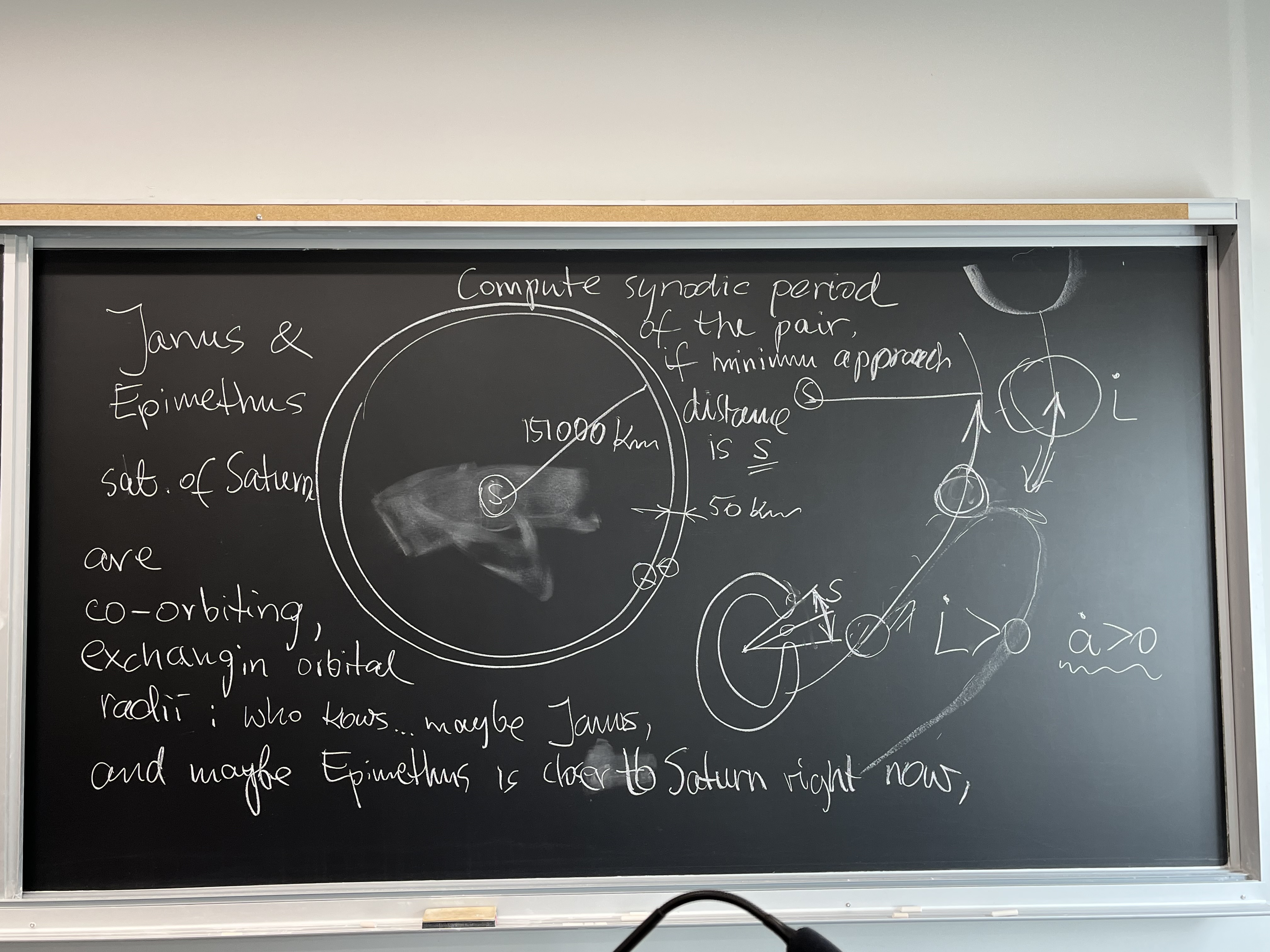
This outlines a problem that we discussed conceptually. Janus and Epimethus are
on orbits spaced by $\Delta a=50$ km only, while their distance from Saturn's
center is about $a=151460$ km. Janus is much more massive, but both satellites
are actually a few times larger than 50 km in size and would have to collide,
if they kept moving on circular orbits. But they don't. A special kind of
coorbital dance called a horseshoe orbit saves them from destruction.
During a close (and slow) approach, they attract each other, which (we showed)
removes the angular momentum from the outer orbit and adds it to whoever (Janus
or Epimethus) occupies the inner orbit at a time. The two orbits drift in
opposite radial directions so fast that they switch outer to inner orbit or
vice versa, and never come closer than distance $s=15000$ km. Knowing the value
of $s$ and the mass of Saturn (from wikipedia), compute the synodic period of
that horseshoe relative orbit! In other words, how often are the satellites
reaching distance $s$ from each other (Janus being ahead of Epimethus)?
SOLUTION hint
Use your knowledge of the synodic period, calculate it first without the
physical interaction of the satellites, based in the given size of both
initial orbits. Then shorten the time interval in proportion to how big
a part of the full circle the "horseshoe clearing" shown in the figure
occupies.
The nominal synodic period follows from the difference of angular speeds
$$|\Omega_2 - \Omega_1 |= |d\Omega/dr|\, \Delta a\; +O((\Delta a/a)^2)
\simeq |d\Omega/dr|\, \Delta a.$$
$$ d\Omega/dr = (-3/2)\, \Omega/a,\;\;\; \mbox{(from Kepler's laws,
$\Omega \sim r^{-3/2}$)}$$
$$P_{syn} = \frac{2\pi}{|\Omega_2-\Omega_1|} =
\frac{2\pi}{\Omega}\;\frac{2a}{3\Delta a}.$$
The fraction $2\pi/\Omega$ is just the orbital period at 151460 km
from Saturn. The orbital encounters are spaced by very many, in fact
about 2000, orbital periods, because $\Delta a \ll a$.
To get a good estimate of the period of the coorbital exchanges,
you need to diminish the nominal $P_{syn}$ by subtracting
$2s/(2\pi a)$ of it,
because the segment that is skipped by one satellite w.r.t. another
is $2s$, relative to the circumference of either orbit (the orbits
have practically the same radius).
COMMENT: The minimum distance $s$ and the orbital spacing $\Delta a$ are
not independent. In fact, you would be able to compute one from the other,
based on the orbital mechanics you know. There are two ways, both
involving the realization that $x\ll y$. The angular mom. conservation
implies $x$-drift rate $\dot{x} = -6/y^2$.
One involves Jacobi energy conservation in Hill's equations,
$E_J = -3/r -3x^2/2 +v^2/2 = const.$.
Another, more direct, way is to solve Hill's equations neglecting
Coriolis force and the x-component of the mutual inter-satellite force, and
later show that this neglect was justified.
$$ \dot{x} = -6/y^2 $$
$$ \dot{y} = -3x/2 $$
Eliminating $dt$, and solving the resulting equation $x\,dx = 4dy/y^2$,
results in a trajectory approximating the round tip of a horseshoe:
$(x_0^2 - x^2) = 8/y $, and consequently the minimum physical distance
$s$ between the satellites given by rescaled coordinate $y$:
$$s/r_L \approx 8 (r_L/\Delta a)^2.$$
Here $r_L$ is the Roche lobe of the dominant satellite (Janus).
Janus-Epimethus orbital spacing is $0.297r_L$, and the computed minimum
distance is $90.28r_L$, or 15300 km, in agreement with observations.
But you were not asked to perform that longer calculation, you were given
both quantities.
To the
ASTC25 course page
Last modified: Apr 2025