P.Art.

Work in progress:

Comparison of two different hydrocodes using Riemann solvers: PPM vs. CLAWPACK

Pawel Artymowicz

I have done some comparisons of the codes VH-1 (PPM in Lagrange + remap back to Euler grid formulation) and CLAW from CLAWPACK/AMRCLAW (unsplit 2nd order algorithm for wave propagation which, unlike the ppm, does not make x- and then y-direction sweeps, i.e. it does't use dimensional splitting.)

The test problem is a 2-d shock tube problem: two layers of high pressure gas along the two walls of a square container, and the highest pressure in the intersecting quadrant. The precise values of initial velocity are taken from CLAW applicactions page. The standard test problem is solved for t=0 to 0.8 on a square uniform grid 200x200. This is a good test of how the codes handle the shocks and the slower shearing post-shock flow, unstable toKelvin-Helmholz (K-H) instability.

This test is described in various places, originally by C.W. Schultz-Rinne (1993, SIAM J Sci Comput. 14, 1394-1414),
(many thanks to Tomek Plewa for this link; and here is a place where its done with CLAW:ftp://amath.washington.edu/pub/rjl/programs/claw/doc/ - download and read note number 15.)

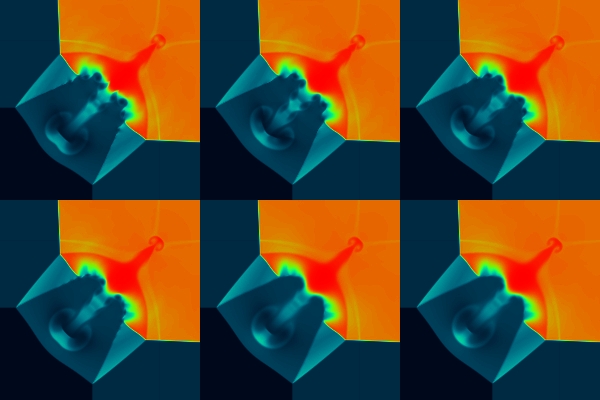
Results of various runs at time t=0.8 will be shown, with panels denoted as

a	b	c
d	e	f

First, the CLAWPACK.

panel	Courant #	cpu time	flux limiters	comments
a	C= 0.15	2180 s (cpu=UltraSparc5)	S S S S	S=superbee flux limiter for all 4 variables (rho, vx,vy, energy; in that order)
b	0.4	824 s	S S S S	strangely, the central parts of the flow do not "interpolate" between panels a & c, although the timestep does.
c	0.9	357 s	S S S S
d	0.9	357 s	S S S M
e	0.9	346 s	S M M M
f	0.9	343 s	M M M M	M=monotonic centered flux limiter

These results show that

timestep is important for some details, but a large value (C. number=0.9) works well.
perfect symmetry w.r.t. diagonal, expected of a correct unsplit method.
somewhat slower execution than naively expected (see below)
well-known difference between MC and super-B (superbee) flux limiters:
the K-H instability becomes visible much sooner in superbee
shock profiles kept sharp.

panel	Courant # [starting value]	cpu time /#steps	dim. splitting	comments
a	C=0.15 [0.03]	793 s /1548	xyyx	K-H instab. delayed for small dt
b	0.3 [0.05]	400 s /794	xyyx
c	0.6 [0.05]	215 s	xyyx	0.6 is the usual Courant # for PPM, and...
d	0.6 [0.6]	198 s	xyyx	..it corresponds to C~0.9 in CLAW (same dt)
e	0.9 [0.9]	148 s /290	xyyx	What happens if C=0.9 is attemped: big wiggle because of dim. splitting!
f	0.9 [0.9]	149 s	yxxy (reversed)	--> mirror reflection of e.

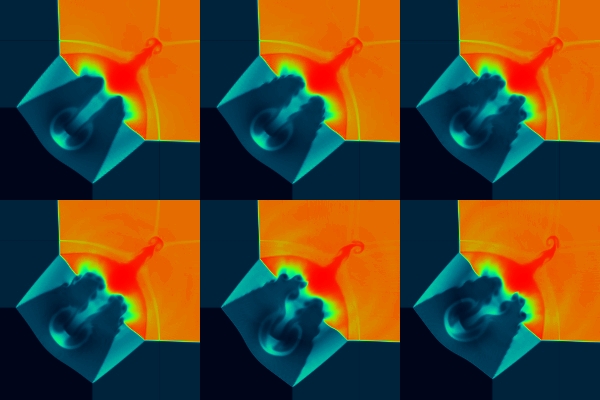
Results

sharpness of shocks similar (2 cells) as above
asymmetries w.r.t. diagonal: strong for large Courant #,
asymmetries become their mirror reflectrions about diagonal when the order of sweeps gets reversed, and are partly cured by taking small dt at the start of the simulation.
whatever the yellow, long linear features are (??), they are slightly sharper in PPM than in CLAW.
if the speed of development of K-H instab. depends on the post-shock oscillation amplitude, then
that quantity will be as large in ppm as in superbee method in CLAW.
dt-->0 sequence in the upper row suggests that post-shock oscillation diminishes at C<<1 or
alternatively that too frequent remapping isn't good for resolution (results in artificial viscosity).
PPM code is single precision, and is 1.75 or so times FASTER than CLAW (which is double precision fortran 77), What does it mean? I expected PPM to be a more complicated algorithm and thus slower, but that's not true (even allowing for faster single precision execution).

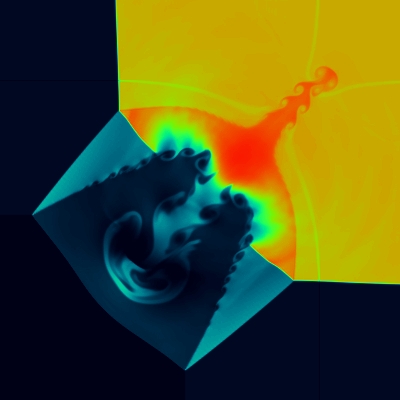
This is C=0.5 (starting from 0.5), t=0.8, VH-1, at 400x400 resolution.

20 Dec. 2000

These models run on a parallel cluster Hydra which is

This way to my home page