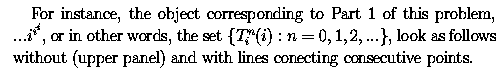
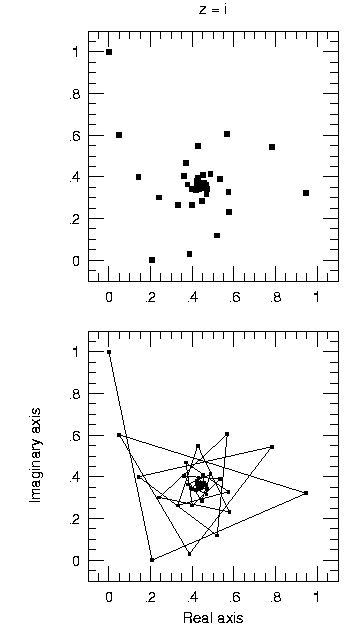
As we see, the approach to the fixed point of the mapping proceeds along a three-armed quasi-spiral such that the consecutive points jump from one arm to the next, counter-clockwise.
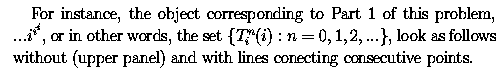

As we see, the approach to the fixed point of the mapping
proceeds along a three-armed quasi-spiral such that the consecutive points
jump from one arm to the next, counter-clockwise.


But think of time needed to survey real Universes!
("Real" and "imaginary" should actually
be used carefully in reference to Universes, in order not to confuse their
literary and mathematical meanings.)
Below we will see how to obtain mathematical objects emulating these astronomical objects:
What if instead of z=i as above we take z=1.6
i? The now familiar 3-armed spiral got tighter!
Some galaxies have spiral arms
about that tightly wrapped. It is of course true that most disk galaxies
show either m=2 pattern, i.e. 2 spiral arms, or many more, but there
are some good examples of the m=3 patterns in galaxies, studied
recently with special image processing techniques by B. Elmegreen et al.
They may be due to the dominance of 3-armed modes of density waves, created
for instance via mode-mode coupling of other waves.
And what if we continue to z=1.71 i? The still 3-armed spiral got even tighter, and now our object resembles a warped disk of a galaxy. Again, this is not the most common bi-symmetric warp but we haven't really been looking for such here.
As we increase the imaginary starting value of our iterated
exponentiation further beyond a critical value between 1.710 and 1.715,
the center of a galaxy, which up to now acted as attractor, suddenly looses
stability and becomes repeller, giving in a sort-of explosion the birth
to 3 separate objects, each of which is a 1-armed galaxy (See the figure
for z=1.72 i below.)
This small group of galaxies is
tight enough in terms of the ratio of distances to object radii, that the
"gravity" of the companions distorts them, creating long tidal tail. Such
tails are the best evidence for the physical interaction of galaxies found
close-by on the sky (which, otherwise might just be a projection effect).
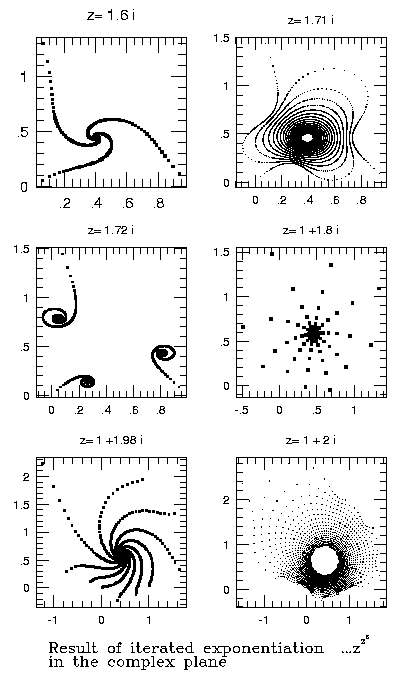
Next, consider in the above figure the remaining 3 objects obtained by following a line in the complex plane parallel but offset by unity from the imaginary axis.
For z=1+1.8 i, we see either a star or alternatively a star cluster (open or globular, depending on imagination). The almost-radial symmetry involved in the picture is misleading, however. In fact, a slight increase of the imaginary component to 1.98 breaks it and leaves us with a 10-armed quasi-spiral. The visual impression is that of an `early' Hubble type (Sa) galaxy with many arms. Unfortunately, in real galaxies of this type the arms are not so regular and continuous throughout the galaxy.
In the vicinity of z=1+2 i (see the illustration above, and the upper-left corner panel in the figure below) we approach the criticality: tight spiral arms wind up so rapidly that the visual impression suggests a drawing of a membrane, not unlike those pictures made to visualize the gravitational potential of a black hole.
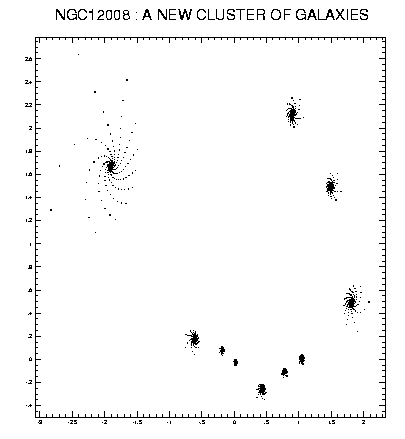
One of the most exciting moments in the exploration of the Complex Universe is the passage through the critical point or critical boundary in the plane located near z=1+2.003 i, when the membrane becomes totally corrugated, for a little moment (not illustrated below) looks like a mess, and then bursts into a cluster of 10 separate 10-armed galaxies.
This cluster has been given an unofficial name NGC 12008 (NGC=New General Catalogue, the well-known catalogue of astronomical objects), although in the retrospect might have been called NGC 12009 as well.
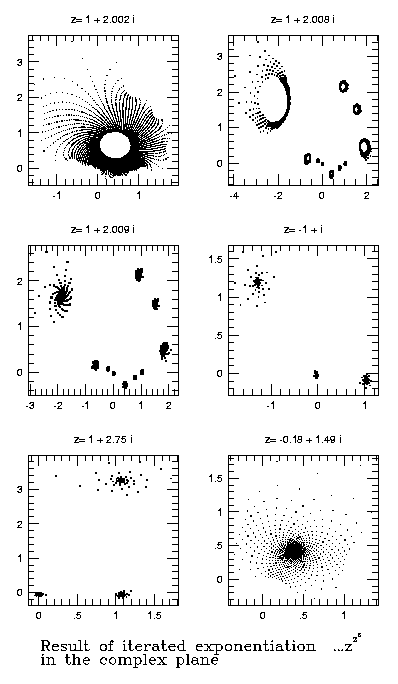
We can see that the high number of objects per cluster or the equality between this number and the internal symmetry of the object (m) are not a necessary feature. For instance, we see at z=-1+ i a small cluster of 3 galaxies with m=8 arms each.
Some objects like that in the lower-right panel above (z=-0.18+ 1.49 i) look like the elliptical galaxies of intermediate degree of flattening (maybe E2 or E3?) .
We now reproduce the detailed discovery photo of the most populous cluster of galaxies found above:
Various other galaxy groups exist, of course, like this one

Some objects, but really few, resemble more Earthly Things, here for example fireworks (though one could argue for a group containing a spiral galaxy, a cluster of black holes, and two Active Galaxies with knotted jetsl as well)
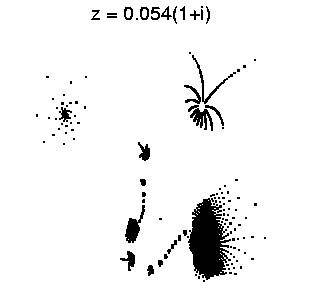
In one sense this is no surprise, because even the much simpler operation of multiplication (squaring) gives rise to an amazing mathematical richness: self-squared Mandelbrot sets, fractals, dragons, and so on [cf. a wonderful book "The fractal geometry of nature" by B. Mandelbrot, first published in 1977].
The strange exponentiated Complex Universe is filled
with objects resembling the known astronomical objects, due to specific
symmetry or lack thereof
(As in certain clusters of objects; the objects seem
to be more symmetric than their clusters.)
Why? I mean, why is it that we rarely recognize more familiar
every-day objects in those iterated maps? Trees, chaotic patterns, animals,
faces... Professional astronomical bias can only provide a partial explanation.
Are these other things so much "more complex"?
The Complex Universe is still a place where no man has gone before...
If you are not bored yet, you can see some brief comments about a mathematical analysis of some aspects of the mathematical objects displayed above.
If you want to see the solution of Part 1 of the puzzle, click here .
You may also return to the home page of the author.
Originally written in 1997