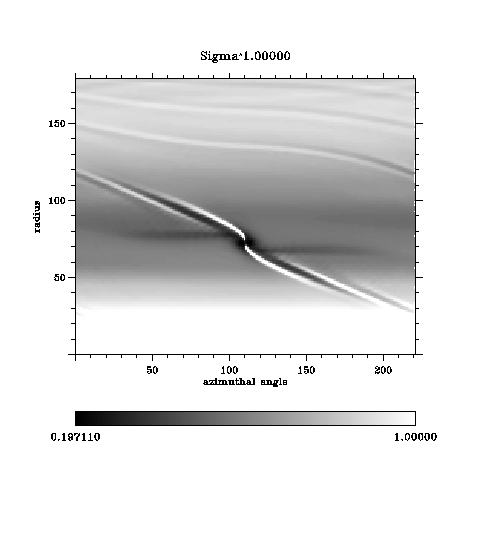
(coordinates in # of grid points, i.e. not a uniform mapping!).
 table of contents
table of contents  next: gap opening
next: gap opening
|
|
mass ratio µ = 3· 10-6 | e = 0 |
|
|
alpha = 0.008 | c/vK = 0.025 |
|
|
resol.: 0.01 x 0.01 | tmax= 100 P |
|
|
negligible | (by assumpt.) |
|
|
da/dt = -2.5 · 10-5 vK (inward) | ta= 75 kyr |
|
|
v= -7.5 · 10-6 vK | tvisc= 250 kyr |
|
|
const. | - |
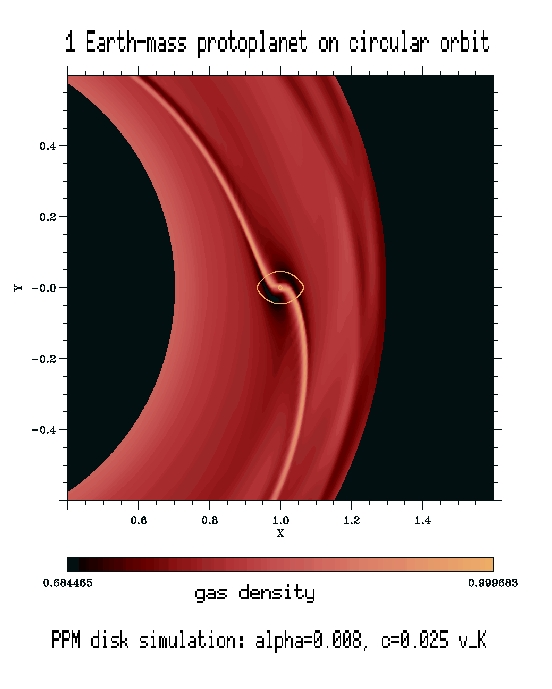
Comments: This simulation shows PPM can handle
such small planets. Wave amplitude of order 10%.
Interesting wake structure is shown below. Despite the
rather thin disk NO LINDBALD RESONACES SEEN directly. Maybe strong non-linear
interaction of m>1 waves that form a wake is the explanation.

(coordinates in # of grid points, i.e. not a uniform
mapping!).
|
|
mass ratio µ = 10-5 | e = 0.01 |
|
|
alpha = 0.008 | c/vK = 0.025 |
|
|
resol.: 0.011 x 0.005 | tmax= 100 P |
|
|
0 | (by assumption) |
|
|
+2.0 · 10-5 vK (outward!) | ta= 94 kyr |
|
|
de2/dt = -2 · 10-6 /tdyn | te= 190 yr |
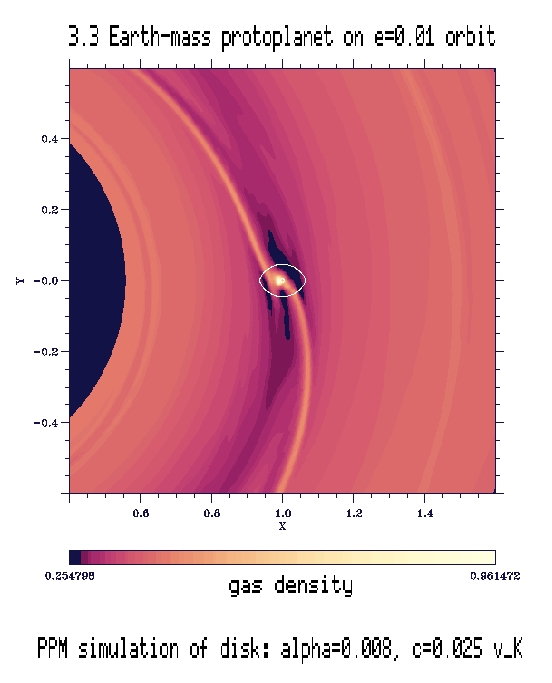
Comments: Eccentricity damped and te
is very short.
Notice how deep a through does this little planet create
in the disk. Inner disk pushes stronger, this is a bit unexpected.
The result is: da/dt= 2.64e-4 (inner disk) + (-2.43e-4)
(outer disk)= +2.14e-5 (whole disk) for t= 96-99 P period.
There is negligible noise in this result (which was checked
by a separate test run with influence of planet on disk forced to be zero;
but there is a slow decay of one-sided effect on da/dt, accompanied by
increased
differential migration as the simulation progresses (dip/gap achieving
equilibrium).
|
|
mass ratio µ = 10-5 | e = 0.01 |
|
|
alpha = 0.008 | c/vK = 0.05 |
|
|
resol.: 0.011 x 0.0055 | tmax= 45 P (120 lower res. ver.) |
|
|
0 | (by assumption) |
|
|
-1.0 · 10-5 vK (-0.5 · 10-5 in low res.) | ta= 188 kyr (380 kyr in lower res. ver.) |
|
|
v=-3.0· 10-5 vK | tvisc= 63 kyr |
|
|
de2/dt = -5 · 10-7 /tdyn | te = 750 yr |
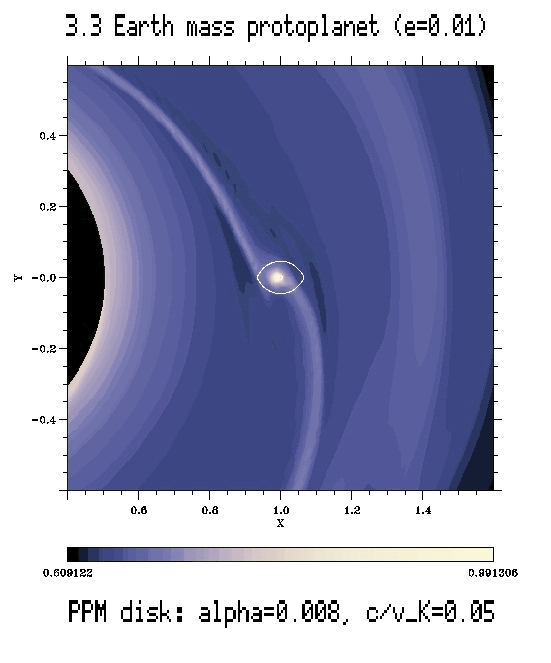
Comments: Eccentricity is damped as expected, although
not necessarily at the analytically predicted rate; The te is
very short. Both inner and outer disk damp e equally.
The migration break-down: da/dt= 7e-5 (inner disk) +
(-8e-5) (outer disk) = -1e-5 (whole disk) in the t=40-43 P interval.
|
|
mass ratio µ = 10-5 | e = 0.01 |
|
|
alpha = 0.004 | c/vK = 0.1 |
|
|
resol.: 0.020 x 0.015 | tmax= 75 P |
|
|
0 | (by assumption) |
|
|
-0.45 · 10-5 vK (inward) | ta= 420 kyr |
|
|
v=-6 · 10-5 vK | tvisc= 31 kyr |
|
|
de2/dt = -1.2 · 10-7 /tdyn | te= 3.1 kyr |
Comments: Eccentricity damped as expected, although
not at the analytically predicted rate; The te is very short,
contributions from inner and outer disk of the same order.
The migration break-down: da/dt= +1.22e-5 (inner disk)
+ (-1.68e-5) (outer disk) = -0.45e-5 (whole disk) in the t= 70-73 P interval.
|
|
mass ratio µ = 3 · 10-5 | e = 0 |
|
|
alpha = 0.006 | c/vK = 0.025 |
|
|
resol.: 0.010 x 0.004 | tmax= 100 P |
|
|
0 | (by assumption) |
|
|
-2.3· 10-5 vK | ta= 84 kyr |
|
|
v=-0.56· 10-5 vK | tvisc= 330 kyr |
|
|
const. | - |
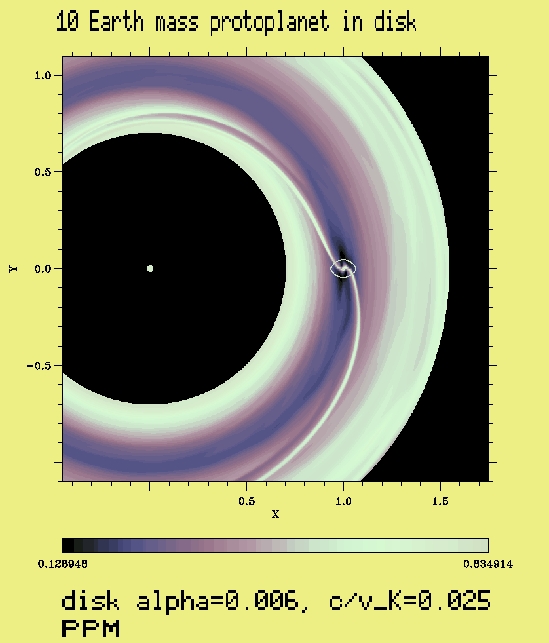
Comments: Eccentricity damped as expected, although
not necessarily at the analytically predicted rate; the same with migration.
Technically, torques and dE/dt from a region outside 1 rL away
from the planet are used here. In this calculation, interestingly, migration
is reduced slightly if material between ½ and 1 rL
is also considered. Usually the innermost region boosts the interaction
from further out.
Notice how deep a through does this planet create in
the disk. It's beginning to look like a gap (density on the opposite
side w.r.t. the planet < ½ that in the surrounding disk).
Standard thermal gap opening criterion: mass ratio>µ
= 3 (c/vK)3 = 4.7 · 10-5, is violated
,
i.e. the gap starts to open disregarding that Roche lobe is smaller than
the disk scale height.
Standard viscous gap opening criterion: mass ratio>µ
= 40 alpha (c/vK)2 = 1.5 · 10-4,
is also violated , i.e. the gap starts to open disregarding that
the viscous torques are supposedly too week to counteract disk viscosity.
Of course, the gap is admittedly open only marginally.
Nevertheless, consider a 20 or 30 Earth mass planet: the viscous criterion
will still be violated, and the gap will then be unambiguously open!
 table of contents
table of contents  next topic: gap opening
next topic: gap opening