Back to the home page of Pawel Artymowicz.

Notes on Beta Pictoris

These notes describe work in progress done by Sally Heap (GSFS), Eric Pantin (Leuven + Saclay), and myself.

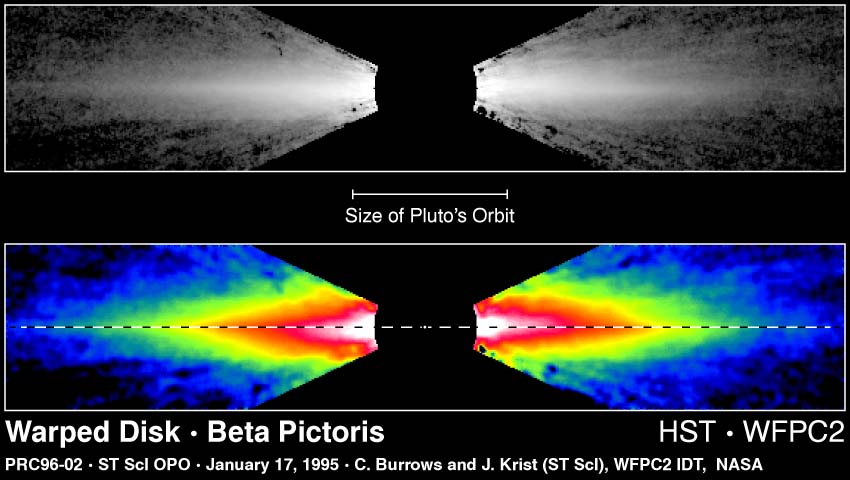
Here is one HST image of a beautiful edge-on dust disk surrounding Beta Pictoris (WFPC2 image obtained by Chris Burrows's group):

There are also newer images showing the disk even better:
the STIS image by Sally Heap's group

Simple parametric model

The STIS image by Sally Heap's group can be modeled with the parametric approach like the one of Artymowicz, Burrows, and Paresce (1989) that worked fine for the interpretation of ground-based images (e.g., Kalas & Jewitt 1995, etc.). The STIS image is of superb quality and allows now direct modeling of the central cavity or gap within about 100 AU from the star. We present here an axisymmetric model.

Model ingredients:

The surface density of dust as a function of radius, or the vertical optical thickness τ(r). This function joins smoothly a r² power law in the center with a r^-3 power law outside (steeper than found before in similar analyses!):
τ(r) = const/[ x^-2*2 + x^+3*2]^½
where x=r/r_m, r_m being the characteristic gap or disk rim radius (density of dust at r=r_m is close to maximum, hence the designation). We find that r_m = 120 AU gives nice results, a value larger than thought appropriate before. (But we fit only the scattered light and forget about thermal radiation here.)

[The above curve is not properly normalized. Similar two-power-law function has been utilized in discussion of the disk physics by Artymowicz (1997, Ann. Rev. Earth Planet. Sci.)]

The vertical dust density profile. We use the following formula for d(τ)/ds, optical thickness per unit length:
d(τ)/ds = const. τ(r)/w exp(-(|z-z_c|/w)^p)
where w = width of the profile in vertical (z) direction, z_c = the coordinate of the maximum dust density, p=power law determining the shape of the vertical profile, and the front constant chosen so that the vertical disk opacity is indeed τ(r).

We used p = 0.7, which corresponds to a central sharp core of density distribution (super-exponential). This is also a departure from previous models, the ancient ones (A+B+P 1989 had p=2, Kalas & Jewitt 1995 had p=1). Beta Pic disk has a dense and thin midplane region (w=1 in the linear plot below):

The disk width changes with radius in the following way:
w(x) = 0.055 r_m x^3/4
which means that the disk is thicker outside than inside but not flaring, and has thickness/radius ratio ~0.06 at 120 AU, which is very similar to that of the solar nebula scale height (at Jupiter distance). Rather thin.

The disk is inclined by a small angle (we used here i=1.3^o) to the plane including the line of sight. (The line of nodes nearly perpendicular to the l.o.s.) The inclination gives the values of z_c throughout the model disk.

Scattering phase function of the dust. We use an analytical approximation to empirical f(θ) for cometary dust compiled from measurements of solar system comets. The formula:
f(θ)=0.3 (0.2 + 0.5 θ)^-3 + 1.4 (θ/3.3)⁴ + 0.2 .

Importantly, alternative phase functions, most notably the Zodiacal Light empirical phase function and some theoretical Mie scatterring functions will be INAPPROPRIATE due to too large a peak in the forward scattering direction. [ZL function from Lamy Perrin 1991 Orig&EvoInterplDust, 163) makes isophotes climb higher instead of going more horizontally near the vertical axis. Other ZL function are less peaked. The cometary function seems to have some of that problem too.
Of course, we know that comet-like planetesimals are good candidates for parent bodies of the dust in Beta Pic, so this is a nice, consistent result. (Notice that Halley comet dust gives the best fit to the 10 micron silicate emission feature of the Beta Pic disk).

Model results:

The isophotes in the STIS image (512 AU by 160 AU):

are reasonably well reproduced by our simple model throughout the image (coloring worked so-so, suggesting larger differences in normalization than they really are):

This isophotal shape agreement is much harder to get than just the agreement of the "midplane brightness" profiles along the spine of the disk:

The solid line is the NE extension of the disk (l.h.s. on images) and the dotted line is the SW side, and the dash-dotted lines are the theoretical model.

Notice the power-law break at 100 AU mentioned already by A+B+P (1989) but first solidly proven by Golimowski, Durance & Clampin (1993) based on adaptive-optics ground-based coronography.