
 Volcano on Io.
Source code
Volcano on Io.
Source code

 Volcano on Io.
Source code
Volcano on Io.
Source code
This page (and not any Quercus/old files scattered on internet or UTSC servers) provides access to all the materials, including up-to-date syllabus, assignments, and some preliminary grades. Quercus will be used for announcements via email, submission of your term work and exams, and for posting of the recordings of lectures and tutorials (in Media Gallery tab).
This page will be modified with new contents as the course progresses. Things highlighted in red are newly added or otherwise important.
Why 1.5? Every student who finished PHYD57 will understand uncomplicated programs (with their arithmetic, iterations/loops, conditional statements, functions/subroutines and their calling, array declaration and usage, pseudorandom numbers, and so on) in both C and Fortran. You will be required to actively express your ideas (a different and much more demanding task!) in only one of those languages. In other words, we want you to acquire passive knowledge of C(++) AND modern Fortran, and an active knowledge of C(++) OR Fortran. By fortran I mean modern fortran: 90, 95, 2003, 2008, or 2015 definitions; they're the same for our purposes. Avoid books/tutorials on really old, earlier FORTRAN versions (IV, 77), even though Fortran, unlike Python, is virtually backward compatible. Starting from Python, Fortran is much easier to learn than C++. Yet many scientific simulations (typically using multi-dimensional arrays) execute somewhat faster when written in Fortran than in C/C++. (Which is remarkable given that it predates C by two decades.)
On the other hand, C(++) is a bit different: more wordy, with more bells and whistles, lower level (we'll discuss what that means), better known and thus more marketable outside academia. A sine qua non for operating system guardians and hackers. Arguably, scientists have a love/hate relationship with C++. They lived together forever, gave life to some great programs, though they weren't meant for each other.
Intel and Nvidia/PGI provide either language in their compiler suites for free to students.
Tutorials are NOT meant for the explanation of Lectures, although sometimes relate to things discussed there. There will be no points for attendance/activity. Negative aspects of not attending and not being active are merciless/automatic enough. We are a small bunch of interested people in this course, whose stile I'd place somewhere between undergraduate and graduate.
Office hours: let's discuss things immediately after the lecture and/or tutorial, I'll try to stay until all topics you want to talk about are discussed or until I really have to go. Other times may be arranged too, depending on my time (I'm teaching one other, larger, astrophysics course.)
The Code of Behaviour on Academic Matters at UofT should be respected. If you have not read it, you may unknowingly find yourself in trouble. This document succinctly defines conduct that constitutes plagiarism, i.e. misrepresentation of authorship, e.g., cheating that the assigned work is yours and original, while you merely rephrase somebody's code by changing its appearance. It is an equal offense to help somebody plagiarize your own work. The Code mentions how any reasonably grounded suspicions must be addressed by your Instructor, by Dept. Chair, and so on. Of course group work on assignment (if explicitly asked for) is a different matter! Read more here.
Practical skills that you will develop include basic familiarity with
Linux operating system. That will be done as one of the first things - you may
want to read on the net about linux before the course starts.
You are strongly encouraged but not required to install
Centos OS or other flavor of linux on your computer
(or use Macos wich is a linux customized by Apple Inc.).
You will have access to one node of a cluster housed in
BV building (there is a banner with a photo of it next to the entrance to DPES
administration office in EV bldg). It has a Centos 6 (linux) system and
basic software, enough for doing a few exercises on your own.
Physical access to the server room is restricted, even I don't have the codes
and key, so if the campus is closed, the IT staff works from home, and the
machine(s) crash because of own reasons or a nasty power outage & they are
down then we're in trouble. But we won't worry in advance, we'll backup
our work on a mirror machine and maybe it will stay up.
In any case, making the research machine(s) available to you
is outside the scope of u/g courses and is an extra benefit to you given by me
without any explicit or implicit promises. I will argue that you should try to
develop codes and even run them on your own machine, which today is more than
feasible. Ask your TA Fergus Horrobin
about some former UTSC students that spectacularly succeeded.
He is one of them.
On your computer, you will sometimes use your Python3, and will be asked to install compiler(s) for HPC languages Fortran and/or C(++), and familiarize yourself with how they function. (If you already know both these languages, then it would be great if you could install Julia compiler and try that new language, created at MIT for purposes consistent with ours, then share your experience.)
In summary, our goals are to help you become a better scientific programmer, able to solve numerically demanding problems on a workstation or a good laptop. While the practice of cluster computing or supercomputing is outside the scope of this undergraduate course, you will hear a lot about it, and even have an option to try it small-scale if you want.
This is a 4th year (upper u/g) course. It explains the issues, tries to interest you in some directions and put you on the right track, but it's your job to move along. This means your own initiative in learning is expected. Great many materials, books and web pages, will be suggested to you, and often you will make your own choice which of them to use. Start very soon, and happy experimenting with the kind of computing you likely haven't experienced yet.
We are fortunate to have Fergus Horrobin as TA/marker. He will mostly do the marking, with some individual email contact.
Our textbooks and materials will be shown in Lecture notes, and will be specific to the current lecture. For instance, Lecture 2 will benefit from reading parts of
N. Schroeghofer, "Lessons in Scientific Computing", CRC 2019.
Please focus on subjects not discussed in introductory course PSCB57, for
instance author's views on different programming languages and how to select
the best combination of two complementary ones. If you read a chapter and
the contents seems really familiar, skip and begin the next chapter.
For L2 and later lectures, and for the knowledge of Fortran, please browse through:
J. Izaac and J. Wang, "Computational Quantum Mechanics", Springer 2018.
and
P. Turner, T. Arildsen, K. Kavanagh, "Applied Scientific Computing with
Python", Springer 2018.
and make sure all the subjects are known to you.
Non-required book for those who want to brush up on Python:
S. Linge, H. Langtangen, "Programming for Computations - Python", Springer 2019 [unlike 1st ed., this 2nd edition uses Python 3]
Guide to literature L1-L5, approximately
Lecture 1
Lecture 2
Lecture 3
Lecture 4
Lecture 5
Lecture 6
Lecture 7
Lecture 8
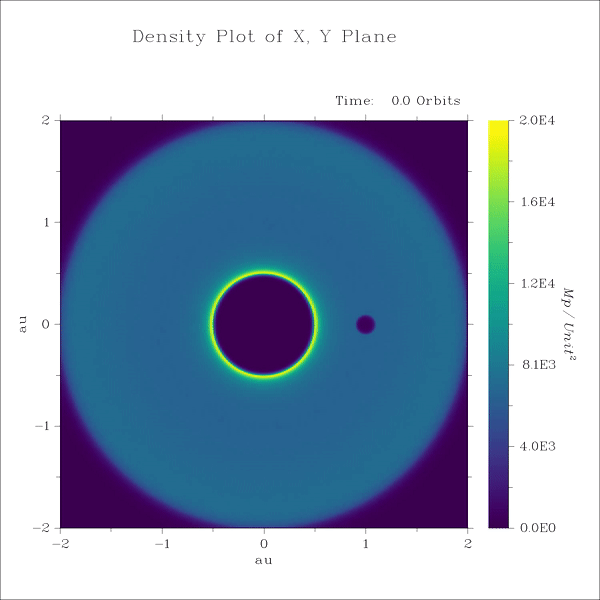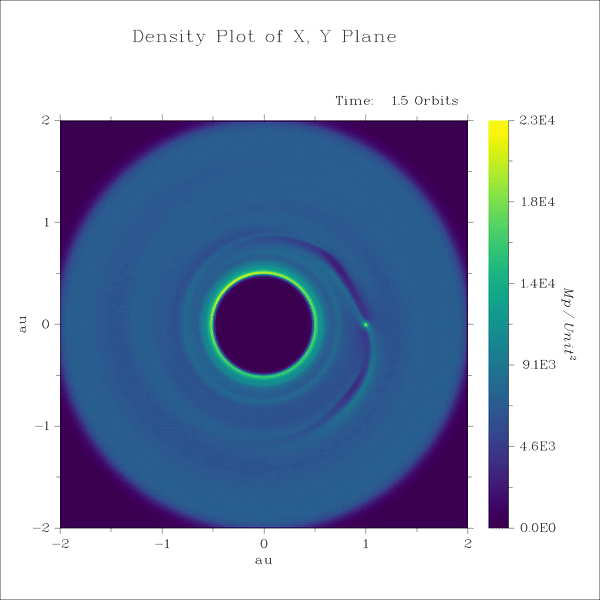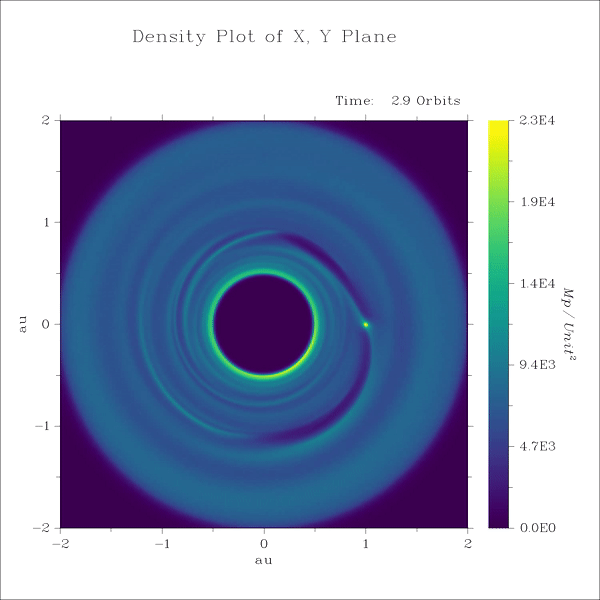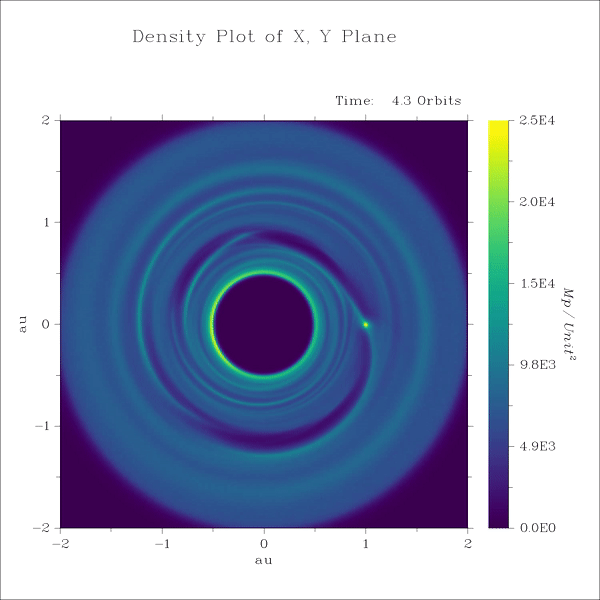
Lecture 9+10
Lecture 11
Lecture 12

Two papers recommended for Neural Networks in application to Astronomy,
NNs-spect.pdf, and
NN-exoplanets.pdf. Also, look at the NN section of the private,
auxiliary page!
Text of assignment set #1. Due 1 Feb.
Text of assignment set #2. Due 17 Feb.
This page: http://planets.utsc.utoronto.ca/~pawel/PHYD57/mid-prep-2022.html will help you prepare for this exam.
By 5 April choose one of the 4
final projects (projects solutions are strictly individual, even if your
choices overlap):
1. Planetary system dynamics. Liapunov stability, statistical study.
2. N-body w/FFT grav: 2-component galaxy + BH (sinking satellite problem)
3. SPH - spiral density waves excited by a protoplanet in a gas disk
4. Mie theory of scattering with application to glories and specters.
Unlike assignments, the project should not be treated as a limited
set of tasks, all specified in the text of the assignment.
Show your initiative, curiosity and ambition,
do interesting computations and tell us about them, even if they
deviate from the suggested descriptions below.
A 8-10 page PDF writeup is also required, and is not the same
as your presentation. Presentation is a slide show, while the writeup is
like an essay or blog entry, starting from the background
on the project that others might not know, methods you used,
code details, tests showing that the code works well and returns meaningful
results in some simple cases, then your results (estimate accuracy!)
and their analysis to draw physical conclusions about the systems in nature.
The writeup unlike the presentation needs to include the list of references.
Data for the fiducial (basic) setup are largely specified in the entry of the catalog http://exoplanet.eu/catalog (enter Trappist-1 into search box). Trappists are Belgian monks making a famous dark beer (visit LCBO if interested). No, they did not observe the exoplanets, but the graduate students doing observations apparently learned a lot about the Trappist beer during their studies. The system has been discovered recently, it has 7 planets, all of them Earth-class and a few in the habitable zone! Find out more about it on the net. Perturbations to the initial conditions away from the given set of parameters will be small and pseudo-random (if they were truly random, you would not be able to repeat the same integration, which you need to do to debug and verify your code).
If you haven't got the knowledge of Kepler problem (2 Body problem) from ASTC25 course to set up initial conditions of the simulation, read about Kepler equation and its iterative solution on the web and ask me questions. Assume that at the start of the calculation, the phase of the motion (fraction of full orbital period the body did from the last pericenter) *and* the time true anomaly theta (the angle you find in the equation of ellipse: r(theta) = a(1-e^2)/(1+e cos theta), are random numbers with uniform distributions (e.g., f between 0 and 2 pi rad). Both statements cannot be simultaneously strictly true, since the motion on ellipse is not uniform in time. But since the Trappist planets are on fairly circular orbits, the assumption is justified in practice. Analytically, i.e. with pen and paper, from the equation of ellipse cited above derive the instantaneous radial and transverse components of velocity vector at any theta, and recalculate to Cartesian coordinates if you use that system for calculations. A hint is that angular momentum per unit mass is a constant in the elliptic motion: r*r*d(theta)/dt = r*v_theta = const. = sqrt(GMa(1-e^2)). therefore v_theta follows very easily from the initial r and the parameters of the ellipse, and v_r, which contains derivative d(theta)/dt, is also easy to compute.
There are actually two ways to quantify the stability, one by watching for close encounters and/or escapes and finding the time at which the change occurs, the other by integrating the shadow systems with miniscule initial deviation of the positions and velocities, to find the Liapunov exponent. I would like you to use the first one and the 2nd as additional indicator if at all. We want to label a system "unstable" if at any point in time (you can check every time step or every now and then, not as often as every time step) planets approach to within 2 Roche lobe radii (see L12) of any of the approaching planets, or if a planet is located further than 2 times the initial distance between the star and outermost planet, or closer to the star than the initial radius of the innermost planet. Ideally, the calculation would then stop and a new variant of the system started. But it's up to you how to optimize & parallelize. Discribe everything in the writeup. Also, in any dynamical calculation describe how you chose the optimum constant time step dt, and how you tested the accuracy of your simulation.
The objective is to write and test the FFT gravity solver first, then test the dynamic integrator (2nd order symplectic, leapfrog), show that both work accurately enough (time step for dynamics integrator must be optimized). Testing involves checking the conservation of those physical quantities that should be constant. Finally, you'll run the code for an extended period of the simulated time, and see what happens with the host galaxy, dwarf galaxy, and their SMBHs. There is no limit how much fun you can have doing the visualization. The minimum is to produce a series of snapshots in 2-D projection(s); plan maximum would be to do animations/videos.
In the phyd57/mie subdirectory you will find some working fortran subroutines such as mie.f90, predicting the spatial distribution of light scattered off a spherical water drop, for a given optical refraction index (or alternatively dielectric constants) of water, and ratio of the particle size to the wavelength of light. [There are in fact 2 separate inputs, radius of a particle and the wavelength of light, since the refractive index of water at a given wavelength can be computed by a separate little function or procedure.] Using that subroutine or translating it into a C(++) procedure, you will assemble a theoretical color image of pilot's glory using 200 separate wavelengths of visible light, and 100 different sizes of water droplets. (You can use Planck function with temperature 3700 K to model the spectrum of a slightly reddened sunlight.) The distribution of water drop sizes will be Gaussian, characterized by a mean size and half-width of distribution (total width will be +-3 half-widths). Fiducial mean size is lambda = 10 micrometers, and half-width of the distribution function is delta = 3 micrometers. Ideally, you will be able to adjust the two parameters of the size distribution until you find a reasonably good match to the chosen picture. At present, nobody knows what size distribution the cloud shown in the picture had. You may be the first person to know it.
If you are interested in Mie theory, although this is not strictly required to master for this project, here you have a book about it. There is a fortran code in the appendix, though my old code is a bit better :-)

• http://www.linfo.org/bit.html . Concept and history of bit (b). Please study it, and follow links to other important basic concepts in that short article, which you will be required to understand and define during exams and quizzes, such as: bitrate, bandwidth, data bus, 32- vs. 64-bit systems, ASCII code, pixels, various powers of 10 in computer lingo, and RAM memory. Note that this online encyclopedia is slightly outdated as (from 2004); in 2019 "current" hardware capabilities are a bit higher (pun intended).
• http://www.linfo.org/byte.html . Concept and history of byte (B). Another bunch of important basic terminology.
•
https://en.wikipedia.org/wiki/Marian_Rejewski .
Are you interested in ENIGMA and its decoding before and during WWII?
Then you have to dig deeper than the related Hollywood
movies, which are at times extremely short on real history (better cf.
Max Hastings, "The secret War: Spies, Codes and Guerillas 1939-1945",
London, 2015). ENIGMA machines were used by Hitler's military for coded
communications between the headquarters and units in the field.
ENIGMA decoding, first achieved in Poland by Marian Rejewski's team,
may eventually have preserved millions of lives,
by saving England from German invasion, tipping the balance in favor of Allies,
and shortening the world war.
After the pre-war Polish cryptologic breakthroughs, hardware devices were built there, implementing the decoding algorithms called Bomba (cryptographic bomb; or "bombe" in top-secret U.S. Army reports of the time). https://en.wikipedia.org/wiki/Bomba_(cryptography). Copies of ENIGMA machines were also built. Eventually an even faster hacking of the gradually more complex combinations of wheels inside ENIGMAs became necessary.
This was undertaken by British government using qualitatively the same approach
as invented by the secret Polish Cipher Bureau. An electromechanical version of
the Polish Bomba was built in Blatchely Park near London by an outstanding pioneer
of computational science Alan Turing. He also created some statistical theory
to aid this work.
The recent biographical movie on
A. Turing and the British Enigma-cracking machinery titled "The imitation
game" distorts the history, as his team is incorrectly given the sole credit
for breaking ENIGMA code. In fact they were neither the first not the last
to come up with essential breakthroughs. For instance, a half-forgotten team
of brilliant engineers of the British Post Office headed by Thomas Flowers
working around the clock for months constructed the specialized Colossus
computer and transferred it to Turing's bureau. That device is shown in the
movie, but was neither Turing's invention nor was tasked with deciphering
ENIGMA codes! Instead, it dealt with other, non-ENIGMA German codes.
Even more powerful machines were developed during the WWWII by American government (Navy), in order to decipher the changed coding procedure used by German submarines. Such devices were the first computers, though not general-purpose electronic computers we have today. They were mostly electromechanical, that is to say based on relays and automatic switches.
As you see, computing from the beginning was and continues to be very very useful. Unfortunately these days it is often used for spying on... you. You do have a smartphone, right? Anyway, enjoy the four ENIGMAtic movies nicely broken down for you on this page .
• http://mason.gmu.edu/~montecin/computer-hist-web.htm Computing history
• https://cs.uwaterloo.ca/~shallit/Courses/134/history.html Computer science history, with further links
• Article where about #1 Fugaku supercomputer is on our way to exaflop computing.
•
https://wiki.python.org/moin/BeginnersGuide/Programmers Introductions of
all sorts to Python language for beginnig coders.
• https://docs.python.org/3.0/reference is Python Language Reference straight from the horses mouth.
• https://docs.python.org/3.0/reference/index.html, Site with docs and resources on Python
•
https://matplotlib.org/3.1.0/tutorials/introductory/pyplot.html.
Tutorial on MatPlotlib and Pyplot
•
https://docs.scipy.org/doc/numpy/index.html. Tutorial and user guide to NumPy
• https://matplotlib.org/3.1.1/tutorials/introductory/pyplot.html. Tutorial on Pyplot (part of Matplotlib based on MATLAB syntax).
• You are encouraged but not required to install Centos OS on your computer, although that is a better option. On art-2 there is an account for you, and you will be shown a password to it, if you later forget it please ask the prof in email. This system has Centos6 OS available for your exercises. To be able to do anything there, you need to learn basic Linux, and if you're connecting from a Windows system, to install an SSH (secure shell) client program PuTTY (or similar) on your machine. The ssh is the way to connect securely and work on a remote linux server, while sftp is a similar client that connects for the purpose of transferring files between two machines on internet. See more in the references cited on our page of references and literature. For instance, cf. p. 52+ in Membrey's book on CentOS.
•
https://www.freecodecamp.org/news/the-best-linux-tutorials/.
Getting Started with Linux, with links to tutorials.
• http://www.linfo.org. Linux info page, including some history pages and explanations of commands. Follow the links.
•
http://tldp.org/HOWTO/Bash-Prog-Intro-HOWTO.html#toc7 . Programming in bash shell.
• https://docs.freebsd.org/44doc/usd/04.csh/paper.html . Programming in csh shell.
•
https://www.wisdomjobs.com/e-university/shell-scripting-tutorial-174.html .
Shell scripting tutorial in different shells.
• Click here . Python vs. Fortran. This discussion on Stackexchange (the often informative resource for coders) shds some light on what programmers think about differences between Python and high-level compiled languages - here Fortran (C/C++ is another).
This article proposes: "It certainly seems likely, in
light of the above, that Fortran will remain the fastest option
for numerical supercomputing for the foreseeable future—at least if 'fast'
refers to the raw speed of compiled code. But there are other reasons for
Fortran’s staying power."
I personally prefer Fortran for demanding research and Python and/or another
scripting language IDL for small tasks and visualization.
C/C++, in which (Unix and) Linux operating systems are
written, is very useful too, as it sometimes provides the
most direct way to tinker with graphics cards (GPUs)
to make them do CUDA. [That is an inside joke for people coming from
my part of Europe. CUDA is the extension of C/C++ (and Fortran) that
directs data transfer to/from CPU and computation on GPU.
Appropriately, the word "cuda" means "miracles" in Slavic
languages and in Hungarian (csodak)]. We deal with such miracles in this
course. C programs are easily callable from Python (as we will learn),
so you can practice multi-language programming and interfacing.
• https://flow.byu.edu/posts/sci-prog-lang provides views similar to my own on the best scientific programming languages (Python+Fortran and C but not C++, Julia in the near future or now at graduate level). Page by Andrew Ning from Flight, Optimization, and Wind Laboratory.
• https://docs.julialang.org/en/v1/. Julia language page
• https://towardsdatascience.com/the-serious-downsides-to-the-julia-language-in-1-0-3-e295bc4b4755 . Advantages and a few gripes about Julia language
• https://www.fortran.com/the-fortran-company-homepage/fortran-tutorials/. Links to Fortran tutorials & other resources.
• https://pages.mtu.edu/~shene/COURSES/cs201/NOTES/fortran.html. Another Fortran tutorial.
• https://www.learn-c.org. Interactive C tutorial.
• https://beginnersbook.com/2014/01/c-tutorial-for-beginners-with-examples. C Tutorial – Learn C Programming with examples. Also C++.
• just for fun. Semi-serious stuff on computer languages. Description of a new language called BS. Combines the worst features of all existing languages.
•
CUDA Fortran blog by Greg Ruetsch (author of one of recommended books on
extra page.)
•
CUDA C blog by Mark Harris, NVIDIA
•
CUDA C presentation - different modes of usage, by Cyril Zeller, NVIDIA.
•
CUDA C Programming Guide. Detailed. Definitive (By Nvidia!). Read the
first 30 pages.
•
CUFFT library description - useful when you need FFT.
When mastered, the world of DSP is yours. Contains code examples.
•
CUDA nvcc compiler manual
•
Paper comparing CUDA in Fortran and C with CPU performance, as a function
of job size.
•
Dr. Dobbs blog CUDA, Supercomputing for the Masses. Links to all 12 pieces. A bit old
but informative.
•
CUDA Fortran compiler, PGI ver.18 User Guide
•
Fortran compiler, PGI ver.18 User Guide
Let's end with a GPU version of a program you already know.
To be compiled with PGI compiler pgf90/95 (only that compiler understands CUDA Fortran
on art-2):
http://planets.utsc.utoronto.ca/~pawel/progD57/tetraDg-3.f95.
• https://www.scientific-computing.com
- if you want to dig (a tiny little bit) below the surface level of buzzwords.
•
https://www.youtube.com/watch?time_continue=414&v=Qm-LLfDPYYQ&feature=emb_logo.
The Coming Age of Extreme Heterogeneity ǀ Jeffrey Vetter. ORNL
• Overview of
desktop supercomputing, past and present (as of 2021).
last modified: Dec 2021